Advertisements
Advertisements
प्रश्न
An aircraft executes a horizontal loop at a speed of 720 km/h with its wings banked at 15°. What is the radius of the loop?
उत्तर १
Here v = 720 km/h = `720xx 5/18` m/s = 200 m/s and angle of banking `theta = 15^@`
From the relation
`tan theta = v^2/"rg"` we have
`r = v^2/(g tan theta) = (200xx200) /(10 xx tan 15^@) = (200xx200)/(10xx0.2679)`
=> r = 14931 m = 14.9 km
उत्तर २
Speed of the aircraft, v = 720 km/h = `720xx5/18 = 200` m/s
Acceleration due to gravity, g = 10 m/s2
Angle of banking, θ = 15°
For radius r, of the loop, we have the relation:
`tan theta = v^2/"rg"`
`r = v^2/(g tan theta)`
`= (200xx200)/(10xx tan 15) = 4000/0.268`
= 14925.37 m
= 14.92 km
APPEARS IN
संबंधित प्रश्न
A rocket with a lift-off mass 20,000 kg is blasted upwards with an initial acceleration of 5.0 m s–2. Calculate the initial thrust (force) of the blast.
A stone of mass m tied to the end of a string revolves in a vertical circle of radius R. The net forces at the lowest and highest points of the circle directed vertically downwards are: [Choose the correct alternative]
| Lowest Point | Highest Point | |
| a) | mg – T1 | mg + T2 |
| b) | mg + T1 | mg – T2 |
| c) | `mg + T1 –(m_v_1^2)/R` | mg – T2 + (`mv_1^2`)/R |
| d) | `mg – T1 – (mv)/R` | mg + T2 + (mv_1^2)/R |
T1 and v1 denote the tension and speed at the lowest point. T2 and v2 denote corresponding values at the highest point.
An object is placed far away from all the objects that can exert force on it. A frame of reference is constructed by taking the origin and axes fixed in this object. Will the frame be necessarily inertial?
A block of mass m is placed on a smooth wedge of inclination θ. The whole system is accelerated horizontally so that the block does not slip on the wedge. The force exerted by the wedge on the block has a magnitude.
Find the reading of the spring balance shown in the following figure. The elevator is going up with an acceleration g/10, the pulley and the string are light and the pulley is smooth.

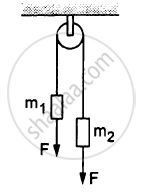
In the following figure, m1 = 5 kg, m2 = 2 kg and F = 1 N. Find the acceleration of either block. Describe the motion of m1 if the string breaks but F continues to act.
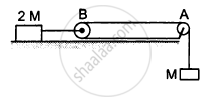
Consider the situation shown in the following figure. Both the pulleys and the string are light and all the surfaces are frictionless. (a) Find the acceleration of the mass M; (b) find the tension in the string; (c) calculate the force exerted by the clamp on the pulley A in the figure.
Write the mathematical form of Newton's second law of motion. State the conditions if any.
A pebble is thrown vertically upwards with a speed of 20 m s-1. How high will it be after 2 s? (Take g = 10 m s-2)
A hockey player is moving northward and suddenly turns westward with the same speed to avoid an opponent. The force that acts on the player is ______.
