Advertisements
Advertisements
प्रश्न
A dietician mixes together two kinds of food in such a way that the mixture contains at least 6 units of vitamin A, 7 units of vitamin B, 11 units of vitamin C and 9 units of vitamin D. The vitamin contents of 1 kg of food X and 1 kg of food Y are given below:
| Vitamin A |
Vitamin B |
Vitamin |
Vitamin D |
|
| Food X Food Y |
1 2 |
1 1 |
1 3 |
2 1 |
One kg food X costs Rs 5, whereas one kg of food Y costs Rs 8. Find the least cost of the mixture which will produce the desired diet.
उत्तर
Let the dietician wishes to mix x kg of food X and y kg of food Y.
Therefore,
As we are given,
| Vitamin A | Vitamin B |
Vitamin C |
Vitamin D | |
| Food X Food Y |
1 2 |
1 1 |
1 3 |
2 1 |
It is given that the mixture should contain at least 6 units of vitamin A, 7 units of vitamin B, 11 units of vitamin C and 9 units of vitamin D.
Therefore, the constraints are
\[x + 2y \geq 6\]
\[x + y \geq 7\]
\[x + 3y \geq 11\]
\[2x + y \geq 9\]
It is given that cost of food X is Rs 5 per kg and cost of food Y is Rs 8 per kg.
Thus, Z = \[5x + 8y\]
Thus, the mathematical formulation of the given linear programmimg problem is
Minimize Z = \[5x + 8y\]
subject to
\[x + 2y \geq 6\]
\[x + y \geq 7\]
\[x + 3y \geq 11\]
\[2x + y \geq 9\]
First, we will convert the given inequations into equations, we obtain the following equations:
x + 2y = 6, x + y = 7, x + 3y =11, 2x + y =9, x = 0 and y = 0.
The line x + 2y = 6 meets the coordinate axis at A1(6, 0) and B1(0, 3). Join these points to obtain the line x + 2y = 6. Clearly, (0, 0) does not satisfies the inequation x + 2y ≥ 6. So, the region in xy-plane that does not contains the origin represents the solution set of the given equation.
The line x + y = 7 meets the coordinate axis at C1(7, 0) and D1(0, 7). Join these points to obtain the line x + y = 7. Clearly, (0, 0) does not satisfies the inequation x + y ≥ 7. So, the region in xy-plane that does not contains the origin represents the solution set of the given equation.
The line x + 3y = 11 meets the coordinate axis at \[E_1 \left( 11, 0 \right)\] and \[F_1 \left( 0, \frac{11}{3} \right)\] Join these points to obtain the line x + 3y = 11.Clearly, (0, 0) does not satisfies the inequation x + 3y ≥ 11. So, the region in xy-plane that does not contains the origin represents the solution set of the given equation.
The line 2x + y = 9 meets the coordinate axis at
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations.
These lines are drawn using a suitable scale.
The feasible region determined by the system of constraints is
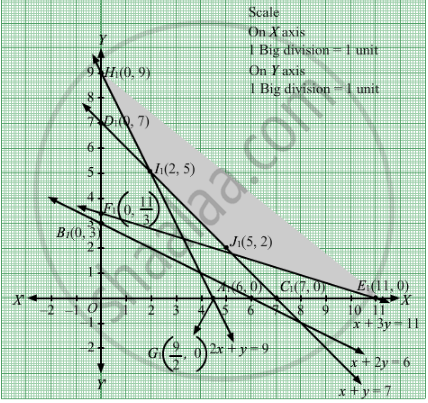
The corner points are H1(0, 9), I1(2 ,5), J1(5, 2), E1(11, 0).
The values of Z at these corner points are as follows
| Corner point | Z= 5x + 8y |
| H1 | 72 |
| I1 | 50 |
| J1 | 41 |
| E1 | 55 |
The minimum value of Z is at J1(5, 2) which is Rs 41.
Hence, cheapest combination of foods will be 5 units of food X and 2 units of food Y.
APPEARS IN
संबंधित प्रश्न
Solve the following L. P. P. graphically:Linear Programming
Minimize Z = 6x + 2y
Subject to
5x + 9y ≤ 90
x + y ≥ 4
y ≤ 8
x ≥ 0, y ≥ 0
Solve the following linear programming problem graphically :
Maximise Z = 7x + 10y subject to the constraints
4x + 6y ≤ 240
6x + 3y ≤ 240
x ≥ 10
x ≥ 0, y ≥ 0
Solve the following L.P.P graphically: Maximise Z = 20x + 10y
Subject to the following constraints x + 2y ≤ 28,
3x + y ≤ 24,
x ≥ 2,
x, y ≥ 0
Solve the following LPP by graphical method:
Minimize Z = 7x + y subject to 5x + y ≥ 5, x + y ≥ 3, x ≥ 0, y ≥ 0
Maximize Z = 50x + 30y
Subject to
\[2x + y \leq 18\]
\[3x + 2y \leq 34\]
\[ x, y \geq 0\]
Minimize Z = 2x + 4y
Subject to
\[x + y \geq 8\]
\[x + 4y \geq 12\]
\[x \geq 3, y \geq 2\]
Maximize Z = x + y
Subject to
\[- 2x + y \leq 1\]
\[ x \leq 2\]
\[ x + y \leq 3\]
\[ x, y \geq 0\]
Maximize Z = 3x1 + 4x2, if possible,
Subject to the constraints
\[x_1 - x_2 \leq - 1\]
\[ - x_1 + x_2 \leq 0\]
\[ x_1 , x_2 \geq 0\]
A diet is to contain at least 80 units of vitamin A and 100 units of minerals. Two foods F1and F2 are available. Food F1 costs Rs 4 per unit and F2 costs Rs 6 per unit one unit of food F1 contains 3 units of vitamin A and 4 units of minerals. One unit of food F2contains 6 units of vitamin A and 3 units of minerals. Formulate this as a linear programming problem and find graphically the minimum cost for diet that consists of mixture of these foods and also meets the mineral nutritional requirements
A farmer mixes two brands P and Q of cattle feed. Brand P, costing ₹250 per bag, contains 2 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing ₹200 per bag contains 1.5 units of nutritional element A, 11.25 units of element B and 3 units of element C. The minimum requirements of nutrients A, B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?
A manufacturer has three machines installed in his factory. machines I and II are capable of being operated for at most 12 hours whereas Machine III must operate at least for 5 hours a day. He produces only two items, each requiring the use of three machines. The number of hours required for producing one unit each of the items on the three machines is given in the following table:
| Item | Number of hours required by the machine | ||
A B |
I | II | III |
| 1 2 |
2 1 |
1 5/4 |
|
He makes a profit of Rs 6.00 on item A and Rs 4.00 on item B. Assuming that he can sell all that he produces, how many of each item should he produces so as to maximize his profit? Determine his maximum profit. Formulate this LPP mathematically and then solve it.
A factory manufactures two types of screws, A and B, each type requiring the use of two machines - an automatic and a hand-operated. It takes 4 minute on the automatic and 6 minutes on the hand-operated machines to manufacture a package of screws 'A', while it takes 6 minutes on the automatic and 3 minutes on the hand-operated machine to manufacture a package of screws 'B'. Each machine is available for at most 4 hours on any day. The manufacturer can sell a package of screws 'A' at a profit of 70 P and screws 'B' at a profit of Rs 1. Assuming that he can sell all the screws he can manufacture, how many packages of each type should the factory owner produce in a day in order to maximize his profit? Determine the maximum profit.
A manufacturer of patent medicines is preparing a production plan on medicines, A and B. There are sufficient raw materials available to make 20000 bottles of A and 40000 bottles of B, but there are only 45000 bottles into which either of the medicines can be put. Further, it takes 3 hours to prepare enough material to fill 1000 bottles of A, it takes 1 hour to prepare enough material to fill 1000 bottles of B and there are 66 hours available for this operation. The profit is Rs 8 per bottle for A and Rs 7 per bottle for B. How should the manufacturer schedule his production in order to maximize his profit?
A small firm manufactures gold rings and chains. The total number of rings and chains manufactured per day is at most 24. It takes 1 hour to make a ring and 30 minutes to make a chain. The maximum number of hours available per day is 16. If the profit on a ring is Rs 300 and that on a chain is Rs 190, find the number of rings and chains that should be manufactured per day, so as to earn the maximum profit. Make it as an LPP and solve it graphically.
There are two types of fertilizers F1 and F2. F1 consists of 10% nitrogen and 6% phosphoric acid and F2 consists of 5% nitrogen and 10% phosphoric acid. After testing the soil conditions, a farmer finds the she needs atleast 14 kg of nitrogen and 14 kg of phosphoric acid for her crop. If F1 costs ₹6/kg and F2 costs ₹5/kg, determine how much of each type of fertilizer should be used so that the nutrient requirements are met at minimum cost. What is the minimum cost?
The value of objective function is maximum under linear constraints ______.
Maximize: z = 3x + 5y Subject to
x +4y ≤ 24 3x + y ≤ 21
x + y ≤ 9 x ≥ 0 , y ≥0
A company manufactures two types of products A and B. Each unit of A requires 3 grams of nickel and 1 gram of chromium, while each unit of B requires 1 gram of nickel and 2 grams of chromium. The firm can produce 9 grams of nickel and 8 grams of chromium. The profit is ₹ 40 on each unit of the product of type A and ₹ 50 on each unit of type B. How many units of each type should the company manufacture so as to earn a maximum profit? Use linear programming to find the solution.
A company manufactures two types of cardigans: type A and type B. It costs ₹ 360 to make a type A cardigan and ₹ 120 to make a type B cardigan. The company can make at most 300 cardigans and spend at most ₹ 72000 a day. The number of cardigans of type B cannot exceed the number of cardigans of type A by more than 200. The company makes a profit of ₹ 100 for each cardigan of type A and ₹ 50 for every cardigan of type B.
Formulate this problem as a linear programming problem to maximize the profit to the company. Solve it graphically and find the maximum profit.
The graph of the inequality 3X − 4Y ≤ 12, X ≤ 1, X ≥ 0, Y ≥ 0 lies in fully in
The minimum value of z = 10x + 25y subject to 0 ≤ x ≤ 3, 0 ≤ y ≤ 3, x + y ≥ 5 is ______.
For the function z = 19x + 9y to be maximum under the constraints 2x + 3y ≤ 134, x + 5y ≤ 200, x ≥ 0, y ≥ 0; the values of x and y are ______.
For the LPP, maximize z = x + 4y subject to the constraints x + 2y ≤ 2, x + 2y ≥ 8, x, y ≥ 0 ______.
The maximum value of z = 3x + 10y subjected to the conditions 5x + 2y ≤ 10, 3x + 5y ≤ 15, x, y ≥ 0 is ______.
The constraints of an LPP are 7 ≤ x ≤ 12, 8 ≤ y ≤ 13. Determine the vertices of the feasible region formed by them.
The maximum of z = 5x + 2y, subject to the constraints x + y ≤ 7, x + 2y ≤ 10, x, y ≥ 0 is ______.
Of all the points of the feasible region for maximum or minimum of objective function the points.
In Corner point method for solving a linear programming problem the first step is to ____________.
In the Corner point method for solving a linear programming problem the second step after finding the feasible region of the linear programming problem and determining its corner points is ____________.
The corner points of the bounded feasible region of a LPP are A(0,50), B(20, 40), C(50, 100) and D(0, 200) and the objective function is Z = x + 2y. Then the maximum value is ____________.
The comer point of the feasible region determined by the following system of linear inequalities:
2x + y ≤ 10, x + 3y ≤ 15, x, y ≥ 0 are (0, 0), (5, 0), (3, 4) and (0, 5). Let x = Px + qx where P, q > 0 condition on P and Q so that the maximum of z occurs at both (3, 4) and (0, 5) is
The maximum value of 2x + y subject to 3x + 5y ≤ 26 and 5x + 3y ≤ 30, x ≥ 0, y ≥ 0 is ______.
The objective function Z = ax + by of an LPP has maximum vaiue 42 at (4, 6) and minimum value 19 at (3, 2). Which of the following is true?
Minimize z = x + 2y,
Subject to x + 2y ≥ 50, 2x – y ≤ 0, 2x + y ≤ 100, x ≥ 0, y ≥ 0.
If x – y ≥ 8, x ≥ 3, y ≥ 3, x ≥ 0, y ≥ 0 then find the coordinates of the corner points of the feasible region.
