Question

A rhombus sheet, whose perimeter is 32 m and whose one diagonal is 10 m long, is painted on both sides at the rate of Rs 5 per m2. Find the cost of painting.

Answer 1

Given that,
Perimeter of a rhombus = 32 m
We know that,
Perimeter of rhombus = 4 × side
⇒ 49 = 32m
⇒ a = 8 m
Let AC = 10 = OA = `1/2`𝐴𝐶
= `1/2`×10
= 5𝑚

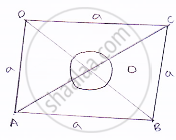
By using Pythagoras theorem:

∴`OB^2=AB^2-OA^2`

`⇒OB=sqrt(AB^2-OA^2)`

`⇒OB=sqrt(8^2-5^2)`

`⇒OB=sqrt(64-25)`

`⇒OB=sqrt(39m)`

Now, BD = 2OB = 2√39𝑚

∴ Area of sheet = `1/2`×𝐵𝐷×𝐴𝐶=`1/2`×2`sqrt(39)xx10sqrt(39)m^2`

∴ Cost of printing on both sides at the rate of Rs 5 per `m^2` = Rs 2 ×10`sqrt(39)`×5
= Rs. 625.00