Advertisements
Advertisements
प्रश्न
ABC एक त्रिभुज है। इसके अभ्यांतर में एक ऐसा बिंदु ज्ञात कीजिए जो ∆ABC के तीनों शीर्षों से समदूरस्थ है।
उत्तर
किसी त्रिभुज का परिकेन्द्र उस त्रिभुज के सभी शीर्षों से सदैव समान दूरी पर होता है। परिकेन्द्र वह बिन्दु है जहाँ त्रिभुज की सभी भुजाओं के लम्ब समद्विभाजक आपस में मिलते हैं।
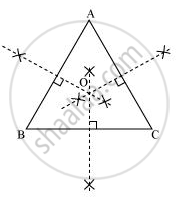
ΔABC में, हम इस त्रिभुज की भुजाओं AB, BC और CA के लंब समद्विभाजक खींचकर परिकेन्द्र ज्ञात कर सकते हैं। O वह बिंदु है जहाँ ये समद्विभाजक आपस में मिल रहे हैं। अतः O वह बिन्दु है जो ΔABC के सभी शीर्षों से समान दूरी पर है।
APPEARS IN
संबंधित प्रश्न
दर्शाइए कि समकोण त्रिभुज में कर्ण सबसे लंबी भुजा होती है।
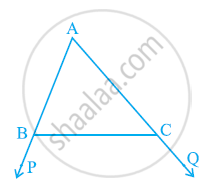
आकृति में, ∆ABC की भुजाओं AB और AC को क्रमशः बिंदुओं P और Q तक बढ़ाया गया है। साथ ही, ∠PBC < ∠QCB, है। दर्शाइए कि: AC > AB है।
आकृति में, ∠B < ∠A और ∠C < ∠D है। दर्शाइए कि: AD < BC है।

AB और CD एक चतुर्भुज ABCD की क्रमशः सबसे छोटी और सबसे लंबी भुजाएँ हैं (देखिए आकृति)। दर्शाइए कि ∠A > ∠C और ∠B > ∠D है।

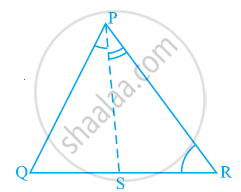
आकृति में, PR > PQ है और PS कोण QPR को समद्विभाजित करता है। सिद्ध कीजिए कि ∠PSR > ∠PSQ है।
दर्शाइए कि एक रेखा पर एक दिए हुए बिंदु से, जो उस रेखा पर स्थित नहीं है, जितने रेखाखंड खींचे जा सकते हैं उनमें लंब रेखाखंड सबसे छोटा होता है।
किसी त्रिभुज के अभ्यांतर में एक ऐसा बिंदु ज्ञात कीजिए जो त्रिभुज की सभी भुजाओं से समदूरस्थ हो।
एक बड़े पार्क में लोग तीन बिंदुओं (स्थानों) पर केंद्रित हैं (देखिए आकृति)।

A: जहाँ बच्चों के लिए फिसल पट्टी और झूले हैं।
B: जिसके पास मानव-निर्मित एक झील है।
C: जो एक बड़े पार्किंग स्थल और बाहर निकलने के रास्ते के निकट है।
एक आइसक्रीम का स्टाल कहाँ लगाना चाहिए ताकि वहाँ लोगों की अधिकतम संख्या पहुँच सके?
(संकेत: स्टॉल को A, B और C से समान दूरी पर होना चाहिए)
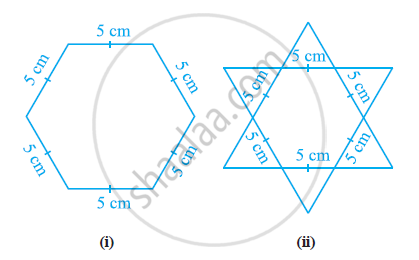
षट्भुजीय और तारे के आकार की रंगोलियों (देखिए आकृति (i) और (ii)] को 1 सेमी भुजा वाले समबाहु त्रिभुजों से भरकर पूरा कीजिए। प्रत्येक स्थिति में, त्रिभुजों की संख्या गिनिए। किसमें अधिक त्रिभुज हैं?
“यदि किसी त्रिभुज के दो कोण और एक भुजा दूसरे त्रिभुज के दो कोण और एक भुजा के बराबर हों, तो दोनों त्रिभुज अवश्य ही सर्वांगसम होने चाहिए।” क्या यह कथन सत्य है? क्यों?
