Advertisements
Advertisements
प्रश्न
Assuming the first statement p and second as q. Write the following statement in symbolic form.
The necessary condition for existence of a tangent to the curve of the function is continuity.
उत्तर
The given statement can also be expressed as ‘If the function is continuous, then the tangent to the curve exists’.
Let p : The function is continuous
q : The tangent to the curve exists.
∴ p → q is the symbolic form of the given statement.
Notes
The answer in the textbook is incorrect.
APPEARS IN
संबंधित प्रश्न
Using truth table prove that p ↔ q = (p ∧ q) ∨ (~p ∧ ~q).
Using the truth table, prove the following logical equivalence :
p ↔ q ≡ (p ∧ q) ∨ (~p ∧ ~q)
Write the following compound statement symbolically.
Angle is neither acute nor obtuse.
Construct the truth table of the following statement pattern.
∼ p ∧ [(p ∨ ∼ q) ∧ q]
Construct the truth table of the following statement pattern.
(p ∨ ∼ q) → (r ∧ p)
If p ∧ q is false and p ∨ q is true, then ______ is not true.
Construct the truth table of the following:
[(p ∧ q) ∨ r] ∧ [∼r ∨ (p ∧ q)]
Determine the truth values of p and q in the following case:
(p ∨ q) is T and (p ∨ q) → q is F
Write the truth value of the following statement.
The Himalayas are the highest mountains but they are part of India in the North East.
Write the following statement in symbolic form.
If Kutub-Minar is in Delhi then Taj-Mahal is in Agra.
Find the truth value of the following statement.
3 is a prime number and an odd number.
If p and q are true and r and s are false, find the truth value of the following compound statement.
[(p ∨ s) → r] ∨ ~ [~ (p → q) ∨ s]
If p and q are true and r and s are false, find the truth value of the following compound statement.
~ [p ∨ (r ∧ s)] ∧ ~ [(r ∧ ~ s) ∧ q]
If p : He swims
q : Water is warm
Give the verbal statement for the following symbolic statement.
q ∧ ~ p
Assuming the first statement p and second as q. Write the following statement in symbolic form.
To be brave is necessary and sufficient condition to climb the Mount Everest.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
It is not true that Ram is tall and handsome.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
If the question paper is not easy then we shall not pass.
If p : Proof is lengthy.
q : It is interesting.
Express the following statement in symbolic form.
Proof is lengthy and it is not interesting.
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
∼ p ∨ q
Rewrite the following statement without using conditional –
(Hint : p → q ≡ ∼ p ∨ q)
If price increases, then demand falls.
Write the negation of the following.
If x ∈ A ∩ B, then x ∈ A and x ∈ B.
Assuming the following statement.
p : Stock prices are high.
q : Stocks are rising.
to be true, find the truth value of the following.
Stock prices are high or stocks are not rising iff stocks are rising.
Write the negation of the following statement.
I will have tea or coffee.
Write the negation of the following statement.
∀ n ∈ N, n + 3 > 9.
Negation of p → (p ˅ ∼ q) is ______
A biconditional statement is the conjunction of two ______ statements.
If p → q is an implication, then the implication ∼ q → ∼ p is called its
Write the following statements in symbolic form
Milk is white if and only if the sky is not blue
Write the negation of p → q
Choose the correct alternative:
A biconditional statement is the conjunction of two ______ statements
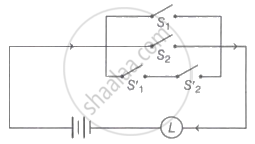
The symbolic form of the following circuit is (where p, q represents switches S1 and S2 closed respectively)
The negation of ∼s ∨ (∼r ∧ s) is equivalent to ______
Let S be a non-empty subset of R. Consider the following statement:
p: There is a rational number x ∈ S such that x > 0. Which of the following statements is the negation of the statement p?
Let p, q and r be any three logical statements. Which of the following is true?
If p : A man is happy, q : A man is rich, then the symbolic form of ‘A man is neither happy nor rich is ______.
From the following set of statements, select two statements which have similar meaning.
- If a man is judge, then he is honest.
- If a man is not a judge, then he is not honest.
- If a man is honest, then he is a judge.
- If a man is not honest, then he is not a judge.
Write the negation of (p `leftrightarrow` q).
Using truth table prove that:
~ (p `leftrightarrow` q) ≡ (p ∧ ~ q) ∨ (q ∧ ~ p)
Construct the truth table for the statement pattern:
[(p → q) ∧ q] → p
