Advertisements
Advertisements
प्रश्न
Construct the truth table of the following statement pattern.
(p ∨ ∼ q) → (r ∧ p)
उत्तर
| p | q | r | ∼ q | p ∨ ∼ q | r ∧ p | (p ∨ ∼ q) → (r ∧ p) |
| T | T | T | F | T | T | T |
| T | T | F | F | T | F | F |
| T | F | T | T | T | T | T |
| T | F | F | T | T | F | F |
| F | T | T | F | F | F | T |
| F | T | F | F | F | F | T |
| F | F | T | T | T | F | F |
| F | F | F | T | T | F | F |
APPEARS IN
संबंधित प्रश्न
Examine whether each of the following statement patterns is a tautology or a contradiction or a contingency.
[~(~p ∧ ~q)] v q
Using truth table, prove the following logical equivalence:
(p ∧ q) → r ≡ p → (q → r)
Using truth table, prove that ~ p ∧ q ≡ (p ∨ q) ∧ ~ p
Using the truth table, prove the following logical equivalence :
p ↔ q ≡ (p ∧ q) ∨ (~p ∧ ~q)
Evaluate: ∫ x . log x dx
Write the following compound statement symbolically.
Hima Das wins gold medal if and only if she runs fast.
Write the following compound statement symbolically.
x is not irrational number but is a square of an integer.
Construct the truth table of the following statement pattern.
[(p → q) ∧ q] → p
Construct the truth table of the following statement pattern.
(p ∧ ∼q) ↔ (p → q)
Construct the truth table of the following statement pattern.
(p ∧ q) ↔ (q ∨ r)
Construct the truth table of the following statement pattern.
p → [∼ (q ∧ r)]
If p ∧ q is false and p ∨ q is true, then ______ is not true.
Construct the truth table of the following:
p → (q → p)
Construct the truth table of the following:
[(p ∧ q) ∨ r] ∧ [∼r ∨ (p ∧ q)]
Construct the truth table of the following:
[(∼p ∨ q) ∧ (q → r)] → (p → r)
Express the following statement in symbolic form.
Mango is a fruit but potato is a vegetable.
Express the following statement in symbolic form.
Milk is white or grass is green.
Express the following statement in symbolic form.
I like playing but not singing.
Express the following statement in symbolic form.
Even though it is cloudy, it is still raining.
Write the truth value of the following statement.
Earth is a planet and Moon is a star.
Write the truth value of the following statement.
A quadratic equation has two distinct roots or 6 has three prime factors.
Write the negation of the following statement.
All men are animals.
Write the negation of the following statement.
− 3 is a natural number.
Write the negation of the following statement.
It is false that Nagpur is capital of Maharashtra
Write the negation of the following statement.
2 + 3 ≠ 5
Write the truth value of the negation of the following statement.
For every x ∈ N, x + 3 < 8.
Write the following statement in symbolic form.
If triangle is equilateral then it is equiangular.
Write the following statement in symbolic form.
Milk is white if and only if the sky is not blue.
Find the truth value of the following statement.
If a joint venture is a temporary partnership, then discount on purchase is credited to the supplier.
Find the truth value of the following statement.
Every accountant is free to apply his own accounting rules if and only if machinery is an asset.
If p and q are true and r and s are false, find the truth value of the following compound statement.
p ∧ (q ∧ r)
If p and q are true and r and s are false, find the truth value of the following compound statement.
~ [(~ p ∨ s) ∧ (~ q ∧ r)]
If p and q are true and r and s are false, find the truth value of the following compound statement.
(p → q) ↔ ~(p ∨ q)
Assuming that the following statement is true,
p : Sunday is holiday,
q : Ram does not study on holiday,
find the truth values of the following statements.
If Sunday is not holiday then Ram studies on holiday.
If p : He swims
q : Water is warm
Give the verbal statement for the following symbolic statement.
q → p
State whether the following statement is True or False:
The negation of 10 + 20 = 30 is, it is false that 10 + 20 ≠ 30.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
The Sun has set and Moon has risen.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
Mona likes Mathematics and Physics.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
3 is prime number if 3 is perfect square number.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
The necessary condition for existence of a tangent to the curve of the function is continuity.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
To be brave is necessary and sufficient condition to climb the Mount Everest.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
It is not true that Ram is tall and handsome.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
Even though it is not cloudy, it is still raining.
If p : Proof is lengthy.
q : It is interesting.
Express the following statement in symbolic form.
Proof is lengthy and it is not interesting.
If p : Proof is lengthy.
q : It is interesting.
Express the following statement in symbolic form.
It is not true that the proof is lengthy but it is interesting.
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
(p ∧ q) ∨ r
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
p → r
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
p→(q ∨ r)
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
p → q
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
(p ∧ q) ∧ ∼ r
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
∼ (p ∨ q) ∧ r
Rewrite the following statement without using conditional –
(Hint : p → q ≡ ∼ p ∨ q)
If demand falls, then price does not increase.
Write the negation of the following.
Ramesh is intelligent and he is hard working.
Write the negation of the following.
An angle is a right angle if and only if it is of measure 90°.
Write the negation of the following.
Kanchanganga is in India and Everest is in Nepal.
Write the negation of the following.
If x ∈ A ∩ B, then x ∈ A and x ∈ B.
Assuming the following statement.
p : Stock prices are high.
q : Stocks are rising.
to be true, find the truth value of the following.
Stock prices are high or stocks are not rising iff stocks are rising.
Rewrite the following statement without using the connective ‘If ... then’.
If a quadrilateral is rhombus then it is not a square.
Rewrite the following statement without using the connective ‘If ... then’.
If 10 − 3 = 7 then 10 × 3 ≠ 30.
Rewrite the following statement without using the connective ‘If ... then’.
If it rains then the principal declares a holiday.
Write the negation of the following statement.
7 is prime number and Tajmahal is in Agra.
Write the negation of the following statement.
∃ x ∈ A, such that x + 5 < 11.
Negation of p → (p ˅ ∼ q) is ______
A biconditional statement is the conjunction of two ______ statements.
The negation of the statement (p ˄ q) `→` (r ˅ ∼ p) is ______.
Without using truth table prove that:
~ (p ∨ q) ∨ (~ p ∧ q) ≡ ~ p
Write the following statements in symbolic form
Even though it is not cloudy, it is still raining
Choose the correct alternative:
Negation of p → (p ˅ ~q) is
Choose the correct alternative:
A biconditional statement is the conjunction of two ______ statements
State whether the following statement is True or False:
The converse of inverse of ~ p → q is q → ~ p
Negation of “Some men are animal “ is ______
Write the negation of the statement “An angle is a right angle if and only if it is of measure 90°”
If (p ∧ ~ r) → (~ p ∨ q) is a false statement, then respective truth values of p, q and r are ______.
Given 'p' and 'q' as true and 'r' as false, the truth values of p v (q ∧ ~r) and (p → r) ∧ q are respectively
If p, q are true statement and r is false statement, then which of the following statements is a true statement.
The symbolic form of the following circuit is (where p, q represents switches S1 and S2 closed respectively)
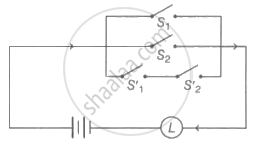
If c denotes the contradiction then the dual of the compound statement ∼p ∧ (q ∨ c) is ______
Let p : 7 is not greater than 4 and q : Paris is in France by two statements. Then ∼(p ∨ q) is the statement ______
The negation of (p ∨ ∼q) ∧ q is ______
The negation of ∼s ∨ (∼r ∧ s) is equivalent to ______
The negation of the statement: "Getting above 95% marks is a necessary condition for Hema to get admission in good college'' is ______
The logical statement (∼p → q) ∧ (q → p) is equivalent to: ______
Conditional of p → q is equivalent to p → ∼ q.
If p : A man is happy, q : A man is rich, then the symbolic form of ‘A man is neither happy nor rich is ______.
Converse of the statement q `rightarrow` p is ______.
Express the following compound statement symbolically:
Delhi is in India but Dhaka is not in Sri Lanka
Express the following compound statement symbolically:
3 + 8 ≥ 12 if and only if 5 × 4 ≤ 25
From the following set of statements, select two statements which have similar meaning.
- If a man is judge, then he is honest.
- If a man is not a judge, then he is not honest.
- If a man is honest, then he is a judge.
- If a man is not honest, then he is not a judge.
If p, q are true statements and r, s are false statements, then write the truth value of the compound statement
(p `→` ∼ r) `→` (q ∧ s)
Using the statements
p: Seema is fat,
q: Seema is happy,
Write the following statements in symbolic form;
- Seema is thin and happy.
- If Seema is fat then she is unhappy.
Using truth table prove that:
~ (p `leftrightarrow` q) ≡ (p ∧ ~ q) ∨ (q ∧ ~ p)
Construct the truth table for the statement pattern:
[(p → q) ∧ q] → p
