Advertisements
Advertisements
प्रश्न
बिंदुओं A(–2, –5) और B(2, 5) को मिलाने वाले रेखाखंड के लंब समद्विभाजक पर स्थित एक बिंदु ______ है।
विकल्प
(0, 0)
(0, 2)
(2, 0)
(–2, 0)
उत्तर
बिंदुओं A(–2, –5) और B(2, 5) को मिलाने वाले रेखाखंड के लंब समद्विभाजक पर स्थित एक बिंदु (0, 0) है।
स्पष्टीकरण:
हम जानते हैं कि, किसी भी रेखाखंड का लंब समद्विभाजक उस खंड को दो बराबर भागों में विभाजित करता है, अर्थात रेखाखंड का लंब समद्विभाजक हमेशा रेखाखंड के मध्य-बिंदु से होकर गुजरता है।
बिंदुओं A(–2, –5) और B(2, 5) को मिलाने वाले रेखाखंड का मध्य-बिंदु
= `((-2 + 2)/2, (-5 + 5)/2)` ...`["चूंकि, किसी भी रेखाखंड का मध्य-बिंदु जो बिंदुओं से गुजरता है" (x_1, y_1) "और" (x_2, y_2) = ((x_1 + x_2)/2, (y_1 + y_2)/2)]`
= (0, 0)
अतः, (0, 0) आवश्यक बिंदु रेखा खंड के लंबवत समद्विभाजक पर स्थित है।
APPEARS IN
संबंधित प्रश्न
सिद्ध कीजिए कि, A(-4, -7), B(-1, 2), C(8, 5) और D(5, -4) समचतुर्भुज ABCD के शीर्ष बिंदु हैं।
निम्नलिखित बिंदुओं को जोड़नेवाले रेखाखंड त्रिभुज बना सकते हैं क्या? यदि त्रिभुज बनता हो तो भुजाओं के आधार पर त्रिभुज का प्रकार लिखिए।
L(6, 4), M(-5, -3), N(-6, 8)
बिंदुओं के निम्नलिखित युग्मों के बीच की दूरी ज्ञात कीजिए:
(a, b), (-a, -b)
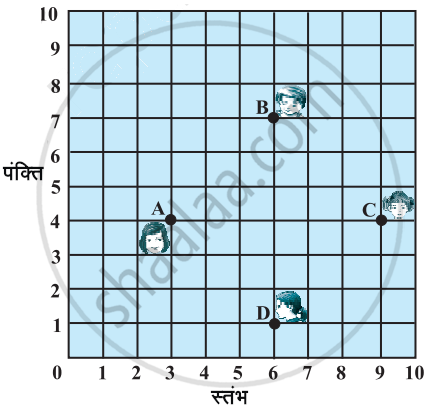
किसी कक्षा में, चार मित्र बिंदुओं A, B, C और D पर बैठे हुए हैं, जैसाकि आकृति में दर्शाया गया है। चंपा और चमेली कक्षा के अंदर आती हैं और कुछ मिनट तक देखने के बाद, चंपा चमेली से पूछती है, 'क्या तुम नहीं सोचती हो कि ABCD एक वर्ग है?' चमेली इससे सहमत नहीं है। दूरी सूत्र का प्रयोग करके, बताइए कि इनमें कौन सही है?
निम्नलिखित बिंदुओं द्वारा बनने वाले चतुर्भुज का प्रकार (यदि कोई है तो) बताइए तथा अपने उत्तर के लिए कारण भी दीजिए:
(4, 5), (7, 6), (4, 3), (1, 2)
बिंदुओं (0, 5) और (–5, 0) के बीच की दूरी ______ है।
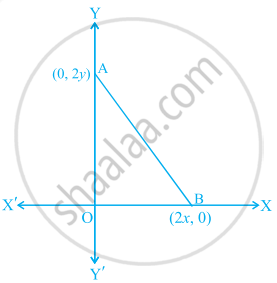
आकृति में दर्शाए गए त्रिभुज AOB के तीनों शीर्षो से समदूरस्थ बिंदु के निर्देशांक ______ हैं।
एक वृत्त का केंद्र मूलबिंदु पर है तथा एक बिंदु P(5, 0) इस वृत्त पर स्थित है। बिंदु Q(6, 8) इस वृत्त के बाहर स्थित है।
बिंदुओं A(2, –2), B(7, 3), C(11, –1) और D(6, –6) को इसी क्रम में लेने पर किस प्रकार का चतुर्भुज बनता है?
यदि बिंदु A(2, – 4), बिंदुओं P(3, 8) और Q(–10, y) से समदूरस्थ है, तो y के मान ज्ञात कीजिए। दूरी PQ भी ज्ञात कीजिए।
