Advertisements
Advertisements
प्रश्न
चित्र में दिए गए दो आरेख दो वर्तुल गतियों के तद्नुरूपी हैं। प्रत्येक आरेख पर वृत्त की त्रिज्या परिक्रमण-काल, आरंभिक स्थिति और परिक्रमण की दिशा दर्शाई गई है। प्रत्येक प्रकरण में, परिक्रमण करते कण के त्रिज्य-सदिश के x-अक्ष पर प्रक्षेप की तदनुरूपी सरल आवर्त गति ज्ञात कीजिए।

उत्तर
(a) माना वृत्त पर गति करता हुआ कण किसी समय पर P से स्थिति A में पहुँच जाता है।
माना ∠POA = θ
AB, बिंदु A से x-अक्ष पर लंब है।
तब ∠ BAO = θ
आवर्तकाल T = 2s
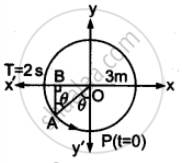
∴ कोणीय वेग ω `= (2pi)/"T" = (2pi)/2 = pi"rad""s"^-1`
∴ `theta = ω"t" = pi"t"`
ΔOAB में, `"sin"theta = "OB"/"OA" = (- x)/3` ...[∵ मूलबिंदु की बाईं ओर x, - ve है।]
∴ x = -3 sin θ या x = -3 sin πt यहाँ x, cm में है।
यही सरल आवर्त गति का अभीष्ट समीकरण है।
(b) 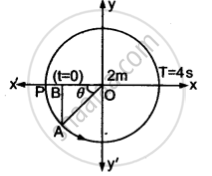
∵ आवर्तकाल T = 4s
∴ कोणीय वेग ω = `(2pi)/"T" = (2pi)/(4"s") = pi/2` rad s-1
माना वर्तुल गति करता हुआ कण t समय में बिंदु P से चलकर A तक पहुँच जाता है।
AB, बिंदु A से x - अक्ष पर लंब है।
माना, ∠BOA = θ तब `theta = ω"t" = (pi"t")/2`
ΔOAB में, `"cos"theta = "OB"/"OA" = - x/2`
∴ x = -2 cos θ
या `x = -2 cos ((pi"t")/2)`
जहाँ x m में है।
यही सरल आवर्त गति का अभीष्ट समीकरण है।
APPEARS IN
संबंधित प्रश्न
नीचे दिए गए उदाहरण में कौन (लगभग) सरल आवर्त गति को तथा कौन आवर्ती परंतु सरल आवर्त गति निरूपित नहीं करते हैं?
पृथ्वी की अपने अक्ष के परितः घूर्णन गति।
नीचे दिए गए उदाहरण में कौन (लगभग) सरल आवर्त गति को तथा कौन आवर्ती परंतु सरल आवर्त गति निरूपित नहीं करते हैं?
किसी U-नली में दोलायमान पारे के स्तंभ की गति।
नीचे दिए गए समय के फलन में कौन (a) सरल आवर्त गति (b) आवर्ती परंतु सरल आवर्त गति नहीं, तथा (c) अनावर्ती गति का निरूपण करते हैं। आवर्ती गति का आवर्तकाल ज्ञात कीजिए: (ω कोई धनात्मक अचर है।)
sin ωt - cos ωt
नीचे दिए गए समय के फलन में कौन (a) सरल आवर्त गति (b) आवर्ती परन्तु सरल आवर्त गति नहीं, तथा (c) अनावर्ती गति का निरूपण करते हैं। प्रत्येक आवर्ती गति का आवर्तकाल ज्ञात कीजिए: (ω कोई धनात्मक अचर है।)
sin3 ωt
नीचे दिए गए समय के फलनों में कौन (a) सरल आवर्त गति (b) आवर्ती परन्तु सरल आवर्त गति नहीं, तथा (e) अनावर्ती गति का निरूपण करते हैं। प्रत्येक आवर्ती गति का आवर्तकाल ज्ञात कीजिए: (ω कोई धनात्मक अचर हैं।)
`3 "cos" (pi/4 - 2 "ωt")`
नीचे दिए गए समय के फलनों में कौन (a) सरल आवर्त गति (b) आवर्ती परन्तु सरल आवर्त गति नहीं, तथा (c) अनावर्ती गति का निरूपण करते हैं। प्रत्येक आवर्ती गति का आवर्तकाल ज्ञात कीजिए: (ω कोई धनात्मक अचर हैं।)
cos ωt + cos 3 ωt + cos 5 ωt
नीचे दिए गए समय के फलनों में कौन (a) सरल आवर्त गति (b) आवर्ती परंतु सरल आवर्त गति नहीं, तथा (c) अनावर्ती गति का निरूपण करते हैं। प्रत्येक आवर्ती गति का आवर्तकाल ज्ञात कीजिए: (ω कोई धनात्मक अचर हैं।)
1 + ωt + ω2t2
नीचे दिए गए किसी कण के त्वरण तथा विस्थापन के बीच संबंधों में से किससे सरल आवर्त गति संबद्ध है:
- a = 0.7 x
- a = -200x²
- a = -10
- a = 100x³
सरल आवर्त गति करते किसी कण की गति का वर्णन नीचे दिए गए विस्थापन फलन द्वारा किया जाता है,
x(t) = A cos (ωt + φ)
यदि कण की आरंभिक (t = 0) स्थिति 1 cm तथा उसका आरंभिक वेग πcms-1 है। तो कण का आयाम तथा आरंभिक कला कोण क्या है? कण की कोणीय आवृत्ति πS-1 है। यदि सरल आवर्त गति का वर्णन करने के लिए कोज्या (cos) फलन के स्थान पर हम ज्या (sin) फलन चुनें; x = B sin (ωt + α), तो उपर्युक्त आरंभिक प्रतिबंधों में कण का आयाम तथा आरंभिक कला कोण क्या होगा?
किसी कण की सरल आवर्त गति के आवर्तकाल का मान उस कण के द्रव्यमान तथा बल-स्थिरांक पर निर्भर करता है: `"T"=2\pi \sqrt { \frac { "m" }{ "k" }]`। कोई सरल लोलक सन्निकट सरल आवर्त गति करता है। तब फिर किसी लोलक का आवर्तकाल लोलक के द्रव्यमान पर निर्भर क्यों नहीं करता?
