Advertisements
Advertisements
प्रश्न
Choose the correct alternative :
The point at which the maximum value of z = x + y subject to the constraints x + 2y ≤ 70, 2x + y ≤ 95, x ≥ 0, y ≥ 0 is
विकल्प
(36, 25)
(20, 35)
(35, 20)
(40, 15)
उत्तर
Z = x + y
The given inequalities are x + 2y ≤ 70, 2x + y ≤ 95.
Consider lines L1 and L2 where L1 : x + 2y = 70 and L2 : 2x + y = 95.
For line L1, plot A (0, 35) and B (70, 0)
For line L2, plot P (0, 95) and Q (47.5, 0).
Solving both lines we get x = 40, y = 15
The coordinates of origin O (0, 0) satisfies both the inequalities.
∴ The required region is on the origin side of both the lines L1 and L2.
As x ≥ 0, y ≥ 0, the feasible region is in the first quadrant.
OQRAO is the required feasible region.
At O (0, 0), z = 0
At Q (47.5, 0), Z = 47.5 + 0 = 47.5
At R (40, 15), Z = 40 + 15 = 55
At A (0, 35), Z = 0 + 35 = 35.
The maximum value of Z is 55 and it occurs at R (40, 15).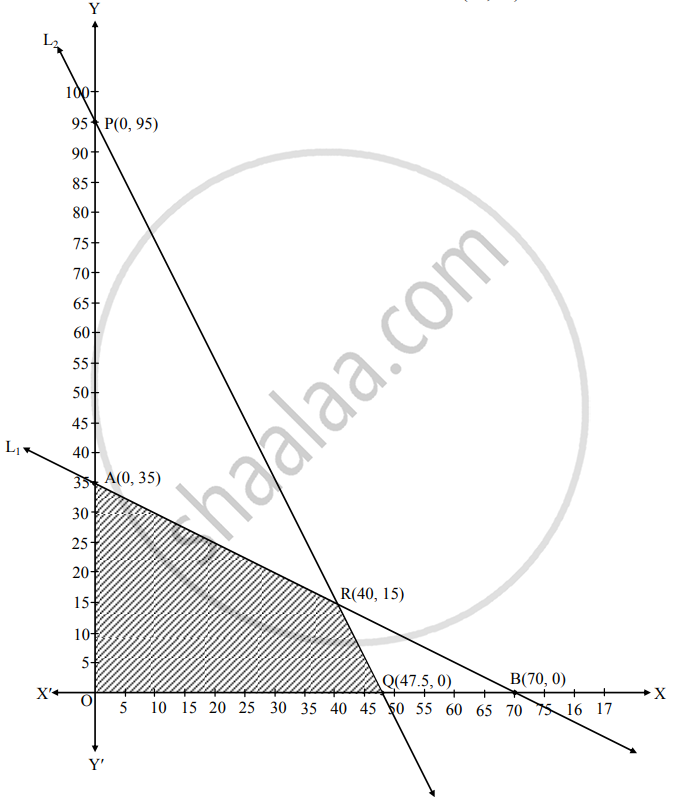
APPEARS IN
संबंधित प्रश्न
A firm manufactures 3 products A, B and C. The profits are Rs 3, Rs 2 and Rs 4 respectively. The firm has 2 machines and below is the required processing time in minutes for each machine on each product :
| Machine | Products | ||
| A | B | C | |
| M1 M2 |
4 | 3 | 5 |
| 2 | 2 | 4 | |
Machines M1 and M2 have 2000 and 2500 machine minutes respectively. The firm must manufacture 100 A's, 200 B's and 50 C's but not more than 150 A's. Set up a LPP to maximize the profit.
Choose the correct alternative:
The value of objective function is maximize under linear constraints.
The constraint that a factory has to employ more women (y) than men (x) is given by _______
Solve the following problem :
Maximize Z = 60x + 50y Subject to x + 2y ≤ 40, 3x + 2y ≤ 60, x ≥ 0, y ≥ 0
Solve the following problem :
A firm manufacturing two types of electrical items A and B, can make a profit of ₹ 20 per unit of A and ₹ 30 per unit of B. Both A and B make use of two essential components, a motor and a transformer. Each unit of A requires 3 motors and 2 transformers and each unit of B requires 2 motors and 4 transformers. The total supply of components per month is restricted to 210 motors and 300 transformers. How many units of A and B should be manufacture per month to maximize profit? How much is the maximum profit?
Choose the correct alternative:
The point at which the minimum value of Z = 8x + 12y subject to the constraints 2x + y ≥ 8, x + 2y ≥ 10, x ≥ 0, y ≥ 0 is obtained at the point
Choose the correct alternative:
The point at which the maximum value of Z = 4x + 6y subject to the constraints 3x + 2y ≤ 12, x + y ≥ 4, x ≥ 0, y ≥ 0 is obtained at the point
State whether the following statement is True or False:
Corner point method is most suitable method for solving the LPP graphically
State whether the following statement is True or False:
The point (6, 4) does not belong to the feasible region bounded by 8x + 5y ≤ 60, 4x + 5y ≤ 40, 0 ≤ x, y
State whether the following statement is True or False:
The graphical solution set of the inequations 0 ≤ y, x ≥ 0 lies in second quadrant
If the feasible region is bounded by the inequations 2x + 3y ≤ 12, 2x + y ≤ 8, 0 ≤ x, 0 ≤ y, then point (5, 4) is a ______ of the feasible region
Smita is a diet conscious house wife, wishes to ensure certain minimum intake of vitamins A, B and C for the family. The minimum daily needs of vitamins A, B, and C for the family are 30, 20, and 16 units respectively. For the supply of the minimum vitamin requirements Smita relies on 2 types of foods F1 and F2. F1 provides 7, 5 and 2 units of A, B, C vitamins per 10 grams and F2 provides 2, 4 and 8 units of A, B and C vitamins per 10 grams. F1 costs ₹ 3 and F2 costs ₹ 2 per 10 grams. How many grams of each F1 and F2 should buy every day to keep her food bill minimum
A wholesale dealer deals in two kinds of mixtures A and B of nuts. Each kg of mixture A contains 60 grams of almonds, 30 grams of cashew and 30 grams of hazel nuts. Each kg of mixture B contains 30 grams of almonds, 60 grams of cashew and 180 grams of hazel nuts. A dealer is contemplating to use mixtures A and B to make a bag which will contain at least 240 grams of almonds, 300 grams of cashew and 540 grams of hazel nuts. Mixture A costs ₹ 8 and B costs ₹ 12 per kg. How many kgs of each mixture should he use to minimize the cost of the kgs
Maximize Z = 5x + 10y subject to constraints
x + 2y ≤ 10, 3x + y ≤ 12, x ≥ 0, y ≥ 0
Minimize Z = 24x + 40y subject to constraints
6x + 8y ≥ 96, 7x + 12y ≥ 168, x ≥ 0, y ≥ 0
Minimize Z = 2x + 3y subject to constraints
x + y ≥ 6, 2x + y ≥ 7, x + 4y ≥ 8, x ≥ 0, y ≥ 0
A linear function z = ax + by, where a and b are constants, which has to be maximised or minimised according to a set of given condition is called a:-
