Advertisements
Advertisements
प्रश्न
Draw an inscribing circle of a regular hexagon of side 5.8 cm.
उत्तर
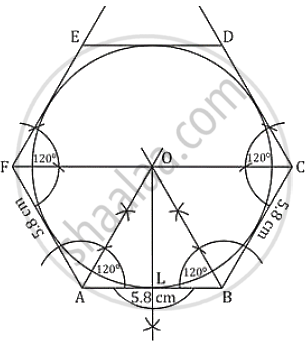
Steps of construction:
- Draw a line segment AB = 5.8 cm.
- At A and B, draw rays making an angle of 120° each and cut off AF = BC = 5.8 cm.
- Again F and C, draw rays making an angle of 120° each and cut off FE = CD = 5.8 cm.
- Join DE. Then ABCDEF is the regular hexagon.
- Draw the bisectors of ∠A and ∠B intersecting each other at O.
- From O, draw OL ⊥ AB.
- With centre O and radius OL, draw a circle which touches the sides of the hexagon.
This is the required in circle of the hexagon.
APPEARS IN
संबंधित प्रश्न
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths. Give the justification of the construction.
In the figure given below, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find:
1) AB.
2) the length of tangent PT.

Draw a circle with centre O and radius 3 cm. Take a point P outside the circle. Draw tangents to the circle from P without using the centre and using only ruler and compasses.
Draw two circles of radii 3.5 cm and 2 cm respectively so that their centres are 6 cm apart. Draw direct common tangents to the circle and show that they are equal in length.
Draw a circle of radius 4 cm. From a point 6 cm away from its centre, construct a pair of tangents to the circle and measure their lengths.
Take a point O on the plane at the paper. With O as center draw a circle of radius 3 cm. Take a point P on this circle and draw a tangent at P.
Draw two lines AB, AC so that ∠ BAC = 40°:
(i) Construct the locus of the center of a circle that touches AB and has a radius of 3.5 cm.
(ii) Construct a circle of radius 35 cm, that touches both AB and AC, and whose center lies within the ∠ BAC.
Draw a circle of radius 4 cm. Take a point P outside the circle without using the center at the circle. Draw two tangents to the circle from point P.
Draw a circle of radius 3 cm and construct a tangent to it from an external point without using the center.
A pair of tangents can be constructed from a point P to a circle of radius 3.5 cm situated at a distance of 3 cm from the centre.
