Question

\[e^\frac{dy}{dx} = x + 1 ; y\left( 0 \right) = 3\]

Answer 1

We have, 
\[ e^\frac{dy}{dx} = x + 1\]
Taking log on both sides, we get
\[\frac{dy}{dx} \log e = \log\left( x + 1 \right)\]
\[ \Rightarrow \frac{dy}{dx} = \log\left( x + 1 \right)\]
\[ \Rightarrow dy = \left\{ \log\left( x + 1 \right) \right\}dx\]
Integrating both sides, we get
\[\int dy = \int\left\{ \log\left( x + 1 \right) \right\}dx\]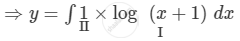

\[ \Rightarrow y = \log \left( x + 1 \right)\int1 dx - \int\left[ \frac{d}{dx}\left( \log x + 1 \right)\int1 dx \right]dx\]
\[ \Rightarrow y = x \log \left( x + 1 \right) - \int\frac{x}{x + 1}dx\]
\[ \Rightarrow y = x \log \left( x + 1 \right) - \int\left( 1 - \frac{1}{x + 1} \right)dx\]
\[ \Rightarrow y = x \log \left( x + 1 \right) - x + \log\left( x + 1 \right) + C . . . . . \left( 1 \right)\]
\[ \text{ It is given that }y\left( 0 \right) = 3 . \]
\[ \therefore 3 = 0 \times \log \left( 0 + 1 \right) - 0 + \log\left( 0 + 1 \right) + C\]
\[ \Rightarrow C = 3\]
\[\text{ Substituting the value of C in }\left( 1 \right), \text{ we get }\]
\[y = x \log \left( x + 1 \right) + \log\left( x + 1 \right) - x + 3\]
\[ \Rightarrow y = \left( x + 1 \right) \log\left( x + 1 \right) - x + 3\]
\[\text{ Hence, }y = \left( x + 1 \right) \log\left( x + 1 \right) - x + 3\text{ is the solution to the given differential equation.}\]