Advertisements
Advertisements
प्रश्न
एक आलू दौड़ (potato race) में, प्रारंभिक स्थान पर एक बाल्टी रखी हुई है, जो पहले आलू से 5m की दूरी पर है, तथा अन्य आलुओं को एक सीधी रेखा में परस्पर 3m की दूरियों पर रखा गया है। इस रेखा पर 10 आलू रखे गए हैं (देखिए आकृति)।

प्रत्येक प्रतियोगी बाल्टी से चलना प्रारंभ करती है, निकटतम आलू को उठाती है, उसे लेकर वापस आकर दौड़कर बाल्टी में डालती है, दूसरा आलू उठाने के लिए वापस दौड़ती है, उसे उठाकर वापस बाल्टी में डालती है, और वह ऐसा तब तक करती रहती है, जब तक सभी आलू बाल्टी में न आ जाएँ। इसमें प्रतियोगी को कुल कितनी दूरी दौड़नी पड़ेगी?
[संकेत: पहले और दूसरे आलुओं को उठाकर बाल्टी में डालने तक दौड़ी गई दूरी = 2 × 5 + 2 × (5 + 3) है।]
उत्तर १
आलू की दूरियाँ इस प्रकार हैं।
5, 8, 11, 14…
यह देखा जा सकता है कि ये दूरियाँ A.P. में हैं।
a = 5
d = 8 − 5
d = 3
`S_n = n/2 [2a+(n-1)d]`
`S_10=10/2[2(5)+(10-1)3]`
= 5 [10 + 9 × 3]
= 5(10 + 27)
= 5(37)
= 185
हर बार उसे बाल्टी में वापस भागना पड़ता है, इसलिए, प्रतियोगी को दौड़ने वाली कुल दूरी दोगुनी होगी।
इसलिए, प्रतियोगी द्वारा दौड़ी जाने वाली कुल दूरी = 2 × 185
= 370 m
वैकल्पिक रूप से,
बाल्टी से आलू की दूरी 5, 8, 11, 14,... है
आलू को इकट्ठा करने के लिए प्रतियोगी द्वारा दौड़ी गई दूरी आलू को रखे जाने की दूरी से दोगुनी है। इसलिए, दौड़ी जाने वाली दूरी हैं
10, 16, 22, 28, 34,...
a = 10
d = 16 − 10
d = 6
S10 =?
`S_10 = 10/2 [2xx10+(10-1)6]`
= 5 [20 + 54]
= 5 (74)
= 370
इसलिए, प्रतियोगी द्वारा दौड़ी जाने वाली कुल दूरी 370 मीटर होगी।
उत्तर २
पहले आलू को उठाकर बाल्टी में डालने तक दौड़ी गई दूरी a1 = 2 × 5 = 10 m = a
दूसरे आलू को उठाकर बाल्टी में डालने तक दौड़ी गई दूरी a2 = 2 × (5 + 3) = 2 × 8 = 16 m
तीसरे आलू को उठाकर बाल्टी में डालने तक दौड़ी गई दूरी a3 = 2 × (8 + 3) = 2 × 11 = 22 m
इस प्रकार दौड़ी गई दूरियाँ क्रमशः 10 m, 16 m, 22 m, ……… एक AP का निर्माण करती हैं।
जहाँ a = 10 m, d = (16 m – 10 m) = 6 m एवं n = 10
चूँकि Sn = `"n"/2` [2a + (n – 1) × d]
⇒ S10 = `10/2` [2 × 10 + (10 – 1) × 6]
= 5 [20 + 54]
= 5 × 74
= 370 m
अतः प्रत्येक प्रतियोगी को कुल 370 m दूरी दौड़नी पड़ेगी।
APPEARS IN
संबंधित प्रश्न
नीचे दिए गए योगफल को ज्ञात कीजिए:
`7 + 10 1/2 + 14 + ... + 84`
एक A.P. में, a = 7 और a13 = 35 दिया है। d और S13 ज्ञात कीजिए।
एक A.P. में, a = 8, an = 62 और Sn = 210 दिया है। n और d ज्ञात कीजिए।
केंद्र A से प्रारंभ करते हुए, बारी-बारी से केंद्रों A और B को लेते हुए, त्रिज्याओं 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm,……. वाले उतरोत्तर अर्धवृत्तों को खींचकर एक सर्पिल (Spiral) बनाया गया है, जैसाकि आकृति में दर्शाया गया है। तेरह क्रमागत अर्धवृत्तों से बने इस सर्पिल की कुल लंबाई क्या है? (π = `22/7` लीजिए।)
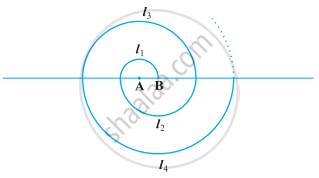
[संकेत: क्रमशः केंद्रों A, B, A, B,... वाले अर्धवृत्तों की लंबाइयाँ l1, l2, l3, l4 हैं।]
एक सीढ़ी के क्रमागत डंडे परस्पर 25 cm की दूरी पर हैं (देखिए आकृति)। डंडों की लंबाई एक समान रूप से घटती जाती हैं तथा सबसे निचले डंडे की लंबाई 45 cm है और सबसे ऊपर वाले डंडे की लंबाई 25 cm है। यदि ऊपरी और निचले डंडे के बीच की दूरी `2 1/2` m है, तो डंडों को बनाने के लिए लकड़ी की कितनी लंबाई की आवश्यकता होगी?
[संकेत: डंडों की संख्या = `250/25 + 1` है।]

योग ज्ञात कीजिए :
`4 - 1/"n" + 4 - 2/"n" + 4 - 3/"n" + ... + "n पदों तक"`
किसी AP में यदि Sn = 3n2 + 5n और ak = 164 है, तो k का मान ज्ञात कीजिए।
ऐसी प्रथम सात संख्याओं का योग ज्ञात कीजिए, जो 2 का गुणज हैं और 9 का भी गुणज हैं।
[संकेत : 2 और 9 का LCM ज्ञात कीजिए।]
ज्ञात कीजिए :
1 और 500 के बीच के उन पूर्णांकों का योग जो 2 के भी गुणज हैं और 5 के भी गुणज हैं।
100 और 200 के बीच के उन पूर्णांकों का योग ज्ञात कीजिए, जो 9 से विभाज्य नहीं हैं।
[संकेत (ii) : ये संख्याएँ होंगी : कुल संख्याएँ– 9 से विभाज्य संख्याएँ]
