Advertisements
Advertisements
प्रश्न
Evaluate the following limit :
`lim_(y -> 1)[(2y - 2)/(root(3)(7 + y) - 2)]`
उत्तर
`lim_(y -> 1)[(2y - 2)/(root(3)(7 + y )- 2)]`
= `lim_(y -> 1) [(2y - 2)/((7 + y)^(1/3) - 8^(1/3))] xx [((7 + y)^(2/3) + (7 + y)^(1/3) 8^(1/3) + 8^(2/3))/((7 + y)^(2/3) + (7 + y)^(1/3) 8^(1/3) + 8^(2/3))]`
= `lim_(y -> 1) ((2y - 2)[(7 + y)^(2/3) + (7 + y)^(1/3) 8^(1/3) + 8^(2/3)])/((7 + y) - 8) ...[because "a" - "b" = ("a"^(1/3) - "b"^(1/3)) ("a"^(2/3) + "a"^(1/3)"b"^(1/3) + "b"^(2/3))]`
= `lim_(y -> 1) (2(y - 1)[(7 + y)^(2/3) + (7 + y)^(1/3) 8^(1/3) + 8^(2/3)])/(y - 1)`
= `lim_(y -> 1) 2[(7 + y)^(2/3) + (7 + y)^(1/3) 8^(1/3) + 8^(2/3)] ...[(because y -> 1"," y ≠ 1","),(therefore y - 1 ≠ 0)]`
= `2[(7 + 1)^(2/3) + (7 + 1)^(1/3) 8^(1/3) + 8^(2/3)]`
= = 2[4 + 4 + 4] ...`[∵ 8^(1/3) = 2 and 8^(2/3) = 4]`
= 24
APPEARS IN
संबंधित प्रश्न
Evaluate the following limit:
`lim_(x -> 3)[sqrt(2x + 6)/x]`
Evaluate the following limit :
`lim_(x -> 1)[(x + x^2 + x^3 + ......... + x^"n" - "n")/(x - 1)]`
Evaluate the following limit :
If `lim_(x -> 5) [(x^"k" - 5^"k")/(x - 5)]` = 500, find all possible values of k.
Evaluate the following limit :
`lim_(x -> 0)[((1 - x)^8 - 1)/((1 - x)^2 - 1)]`
Evaluate the following limit :
`lim_(x -> 0)[(root(3)(1 + x) - sqrt(1 + x))/x]`
Evaluate the following limit :
`lim_(x -> 7) [(x^3 - 343)/(sqrt(x) - sqrt(7))]`
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 2) f(x)` where `f(x) = {{:(4 - x",", x ≠ 2),(0",", x = 2):}`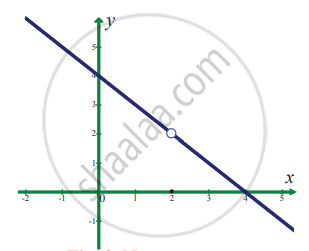
If the limit of f(x) as x approaches 2 is 4, can you conclude anything about f(2)? Explain reasoning
Verify the existence of `lim_(x -> 1) f(x)`, where `f(x) = {{:((|x - 1|)/(x - 1)",", "for" x ≠ 1),(0",", "for" x = 1):}`
Evaluate the following limits:
`lim_(x -> 5) (sqrt(x + 4) - 3)/(x - 5)`
Evaluate the following limits:
`lim_(x -> 0) (sqrt(x^2 + 1) - 1)/(sqrt(x^2 + 16) - 4)`
Evaluate the following limits:
`lim_(x -> 2) (2 - sqrt(x + 2))/(root(3)(2) - root(3)(4 - x))`
Evaluate the following limits:
`lim_(x - 0) (sqrt(1 + x^2) - 1)/x`
Evaluate the following limits:
`lim_(x -> 0) (sqrt(1 - x) - 1)/x^2`
Find the left and right limits of f(x) = tan x at x = `pi/2`
Evaluate the following limits:
`lim_(x -> oo) (x^3 + x)/(x^4 - 3x^2 + 1)`
Evaluate the following limits:
`lim_(x -> oo) (x^4 - 5x)/(x^2 - 3x + 1)`
Evaluate the following limits:
`lim_(x -> oo) (1 + x - 3x^3)/(1 + x^2 +3x^3)`
A tank contains 5000 litres of pure water. Brine (very salty water) that contains 30 grams of salt per litre of water is pumped into the tank at a rate of 25 litres per minute. The concentration of salt water after t minutes (in grams per litre) is C(t) = `(30"t")/(200 + "t")`. What happens to the concentration as t → ∞?
Evaluate the following limits:
`lim_(x -> oo)(1 + "k"/x)^("m"/x)`
Evaluate the following limits:
`lim_(x -> 0) (2 "arc"sinx)/(3x)`
Evaluate the following limits:
`lim_(x-> 0) (1 - cos x)/x^2`
Evaluate the following limits:
`lim_(x -> 0) (2^x - 3^x)/x`
Evaluate the following limits:
`lim_(x -> 0) (1 - cos^2x)/(x sin2x)`
Evaluate the following limits:
`lim_(x -> 0) (sqrt(2) - sqrt(1 + cosx))/(sin^2x)`
Evaluate the following limits:
`lim_(x -> 0) ("e"^("a"x) - "e"^("b"x))/x`
Evaluate the following limits:
`lim_(x -> ) (sinx(1 - cosx))/x^3`
Choose the correct alternative:
`lim_(x - pi/2) (2x - pi)/cos x`
Choose the correct alternative:
If `f(x) = x(- 1)^([1/x])`, x ≤ 0, then the value of `lim_(x -> 0) f(x)` is equal to
Choose the correct alternative:
If `lim_(x -> 0) (sin "p"x)/(tan 3x)` = 4, then the value of p is
Choose the correct alternative:
`lim_(x -> 0) ("e"^tanx - "e"^x)/(tan x - x)` =
If `lim_(x->1)(x^5-1)/(x-1)=lim_(x->k)(x^4-k^4)/(x^3-k^3),` then k = ______.
`lim_(x -> 0) ((2 + x)^5 - 2)/((2 + x)^3 - 2)` = ______.
If `lim_(x -> 1) (x + x^2 + x^3|+ .... + x^n - n)/(x - 1)` = 820, (n ∈ N) then the value of n is equal to ______.
