Advertisements
Advertisements
प्रश्न
Evaluate the following limit :
If `lim_(x -> 5) [(x^"k" - 5^"k")/(x - 5)]` = 500, find all possible values of k.
उत्तर
`lim_(x -> 5) [(x^"k" - 5^"k")/(x - 5)]` = 500
∴ k(5)k–1 = 500 ...`[because lim_(x -> "a") (x^"n" - "a"^"n")/(x - "a") = "na"^("n" - 1)]`
∴ k(5)k–1 = 4 × 125
∴ k(5)k–1 = 4 × (5)3
∴ k(5)k–1 = 4 × (5)4–1
Comparing both sides, we get
k = 4
APPEARS IN
संबंधित प्रश्न
Evaluate the following limit:
`lim_(z -> -3) [sqrt("z" + 6)/"z"]`
Evaluate the following limit:
`lim_(y -> -3) [(y^5 + 243)/(y^3 + 27)]`
Evaluate the following limit:
`lim_(x -> 3)[sqrt(2x + 6)/x]`
Evaluate the following limit :
`lim_(x -> 1)[(x + x^2 + x^3 + ......... + x^"n" - "n")/(x - 1)]`
Evaluate the following limit :
`lim_(x -> 7) [(x^3 - 343)/(sqrt(x) - sqrt(7))]`
In the following example, given ∈ > 0, find a δ > 0 such that whenever, |x – a| < δ, we must have |f(x) – l| < ∈.
`lim_(x -> 2)(2x + 3)` = 7
In the following example, given ∈ > 0, find a δ > 0 such that whenever, |x – a| < δ, we must have |f(x) – l| < ∈.
`lim_(x -> -3) (3x + 2)` = – 7
Evaluate the following :
Find the limit of the function, if it exists, at x = 1
f(x) = `{(7 - 4x, "for", x < 1),(x^2 + 2, "for", x ≥ 1):}`
In problems 1 – 6, using the table estimate the value of the limit
`lim_(x -> 0) (sqrt(x + 3) - sqrt(3))/x`
| x | – 0.1 | – 0.01 | – 0.001 | 0.001 | 0.01 | 0.1 |
| f(x) | 0.2911 | 0.2891 | 0.2886 | 0.2886 | 0.2885 | 0.28631 |
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 1) f(x)` where `f(x) = {{:(x^2 + 2",", x ≠ 1),(1",", x = 1):}`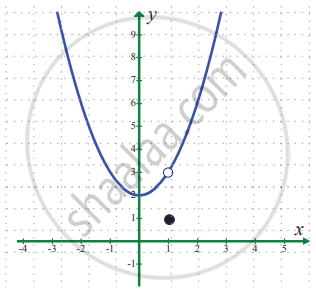
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 3) 1/(x - 3)`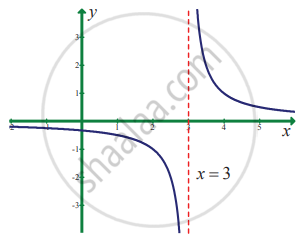
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 5) |x - 5|/(x - 5)`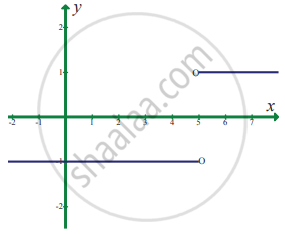
Sketch the graph of a function f that satisfies the given value:
f(0) is undefined
`lim_(x -> 0) f(x)` = 4
f(2) = 6
`lim_(x -> 2) f(x)` = 3
If the limit of f(x) as x approaches 2 is 4, can you conclude anything about f(2)? Explain reasoning
Evaluate the following limits:
`lim_("h" -> 0) (sqrt(x + "h") - sqrt(x))/"h", x > 0`
Evaluate the following limits:
`lim_(x -> 1) (sqrt(x) - x^2)/(1 - sqrt(x))`
Evaluate the following limits:
`lim_(x -> 0) (sqrt(1 - x) - 1)/x^2`
Evaluate the following limits:
`lim_(x -> 3) (x^2 - 9)/(x^2(x^2 - 6x + 9))`
Evaluate the following limits:
`lim_(x -> oo) (x^4 - 5x)/(x^2 - 3x + 1)`
Evaluate the following limits:
`lim_(x -> oo) (1 + x - 3x^3)/(1 + x^2 +3x^3)`
Show that `lim_("n" -> oo) 1/1.2 + 1/2.3 + 1/3.4 + ... + 1/("n"("n" + 1))` = 1
A tank contains 5000 litres of pure water. Brine (very salty water) that contains 30 grams of salt per litre of water is pumped into the tank at a rate of 25 litres per minute. The concentration of salt water after t minutes (in grams per litre) is C(t) = `(30"t")/(200 + "t")`. What happens to the concentration as t → ∞?
Evaluate the following limits:
`lim_(x -> 0)(1 + x)^(1/(3x))`
Evaluate the following limits:
`lim_(x -> 0) (sin^3(x/2))/x^2`
Evaluate the following limits:
`lim_(x -> 0) (sinalphax)/(sinbetax)`
Evaluate the following limits:
`lim_(x -> 0) (tan 2x)/x`
Evaluate the following limits:
`lim_(x -> oo) x [3^(1/x) + 1 - cos(1/x) - "e"^(1/x)]`
Evaluate the following limits:
`lim_(x -> pi) (sin3x)/(sin2x)`
Evaluate the following limits:
`lim_(x -> pi) (1 + sinx)^(2"cosec"x)`
Evaluate the following limits:
`lim_(x -> 0) (sqrt(1 + sinx) - sqrt(1 - sinx))/tanx`
Evaluate the following limits:
`lim_(x -> ) (sinx(1 - cosx))/x^3`
Choose the correct alternative:
`lim_(x -> 0) sqrt(1 - cos 2x)/x`
Choose the correct alternative:
`lim_(theta -> 0) (sinsqrt(theta))/(sqrt(sin theta)`
Choose the correct alternative:
`lim_(x -> 3) [x]` =
`lim_(x→-1) (x^3 - 2x - 1)/(x^5 - 2x - 1)` = ______.
`lim_(x→∞)((x + 7)/(x + 2))^(x + 4)` is ______.
The value of `lim_(x rightarrow 0) (sqrt((1 + x^2)) - sqrt(1 - x^2))/x^2` is ______.
