Advertisements
Advertisements
प्रश्न
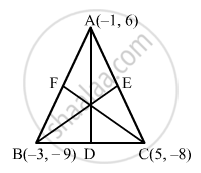
Find the equations of the medians of a triangle, the coordinates of whose vertices are (−1, 6), (−3, −9) and (5, −8).
उत्तर
Let A (−1, 6), B (−3, −9) and C (5, −8) be the coordinates of the given triangle.
Let D, E and F be midpoints of BC, CA and AB, respectively.
So, the coordinates of D, E and F are
\[D \equiv \left( \frac{- 3 + 5}{2}, \frac{- 9 - 8}{2} \right) = \left( 1, \frac{- 17}{2} \right)\]
\[E \equiv \left( \frac{- 1 + 5}{2}, \frac{6 - 8}{2} \right) = \left( 2, - 1 \right)\]
\[F \equiv \left( \frac{- 1 - 3}{2}, \frac{6 - 9}{2} \right) = \left( - 2, - \frac{3}{2} \right)\]
Median AD passes through
\[A \left( - 1, 6 \right) \text { and } D \left( 1, - \frac{17}{2} \right)\]
So, its equation is
\[y - 6 = \frac{- \frac{17}{2} - 6}{1 + 1}\left( x + 1 \right)\]
\[ \Rightarrow 4y - 24 = - 29x - 29\]
\[ \Rightarrow 29x + 4y + 5 = 0\]
Median BE passes through \[B \left( - 3, - 9 \right) \text { and } E \left( 2, - 1 \right)\]
So, its equation is
\[y + 9 = \frac{- 1 + 9}{2 + 3}\left( x + 3 \right)\]
\[ \Rightarrow 5y + 45 = 8x + 24\]
\[ \Rightarrow 8x - 5y - 21 = 0\]
Median CF passes through
\[C \left( 5, - 8 \right) \text { and } F \left( - 2, - \frac{3}{2} \right)\]
So, its equation is
\[y + 8 = \frac{- \frac{3}{2} + 8}{- 2 - 5}\left( x - 5 \right)\]
\[ \Rightarrow - 14y - 112 = 13x - 65\]
\[ \Rightarrow 13x + 14y + 47 = 0\]
APPEARS IN
संबंधित प्रश्न
Find the equation of the line parallel to x-axis and passing through (3, −5).
Find the equation of the line perpendicular to x-axis and having intercept − 2 on x-axis.
Draw the lines x = − 3, x = 2, y = − 2, y = 3 and write the coordinates of the vertices of the square so formed.
Find the equation of the straight line passing through (−2, 3) and inclined at an angle of 45° with the x-axis.
Find the equation of the straight line passing through (3, −2) and making an angle of 60° with the positive direction of y-axis.
Find the equation of the straight lines passing through the following pair of point :
(a, b) and (a + c sin α, b + c cos α)
Find the equation of the straight lines passing through the following pair of point :
(0, −a) and (b, 0)
The length L (in centimeters) of a copper rod is a linear function of its celsius temperature C. In an experiment, if L = 124.942 when C = 20 and L = 125.134 when C = 110, express L in terms of C.
Find the equations to the straight lines which go through the origin and trisect the portion of the straight line 3 x + y = 12 which is intercepted between the axes of coordinates.
A straight line passes through the point (α, β) and this point bisects the portion of the line intercepted between the axes. Show that the equation of the straight line is \[\frac{x}{2 \alpha} + \frac{y}{2 \beta} = 1\].
Find the equation of the straight line passing through the point (2, 1) and bisecting the portion of the straight line 3x − 5y = 15 lying between the axes.
The straight line through P (x1, y1) inclined at an angle θ with the x-axis meets the line ax + by + c = 0 in Q. Find the length of PQ.
Find the equation of straight line passing through (−2, −7) and having an intercept of length 3 between the straight lines 4x + 3y = 12 and 4x + 3y = 3.
Three sides AB, BC and CA of a triangle ABC are 5x − 3y + 2 = 0, x − 3y − 2 = 0 and x + y − 6 = 0 respectively. Find the equation of the altitude through the vertex A.
Find the equation of the line passing through the intersection of the lines 2x + y = 5 and x + 3y + 8 = 0 and parallel to the line 3x + 4y = 7.
Find the equation of a line passing through the point (2, 3) and parallel to the line 3x − 4y + 5 = 0.
Find the equation of the straight line through the point (α, β) and perpendicular to the line lx + my + n = 0.
Find the distance of the point (1, 2) from the straight line with slope 5 and passing through the point of intersection of x + 2y = 5 and x − 3y = 7.
Find the equation of the straight lines passing through the origin and making an angle of 45° with the straight line \[\sqrt{3}x + y = 11\].
Find the equations to the sides of an isosceles right angled triangle the equation of whose hypotenues is 3x + 4y = 4 and the opposite vertex is the point (2, 2).
Find the equations of the two straight lines through (1, 2) forming two sides of a square of which 4x+ 7y = 12 is one diagonal.
Find the equation of the straight line drawn through the point of intersection of the lines x + y = 4 and 2x − 3y = 1 and perpendicular to the line cutting off intercepts 5, 6 on the axes.
Prove that the family of lines represented by x (1 + λ) + y (2 − λ) + 5 = 0, λ being arbitrary, pass through a fixed point. Also, find the fixed point.
Find the equation of the straight line passing through the point of intersection of 2x + y − 1 = 0 and x + 3y − 2 = 0 and making with the coordinate axes a triangle of area \[\frac{3}{8}\] sq. units.
Find the equation of the straight line which passes through the point of intersection of the lines 3x − y = 5 and x + 3y = 1 and makes equal and positive intercepts on the axes.
Find the equations of the lines through the point of intersection of the lines x − 3y + 1 = 0 and 2x + 5y − 9 = 0 and whose distance from the origin is \[\sqrt{5}\].
If the diagonals of the quadrilateral formed by the lines l1x + m1y + n1 = 0, l2x + m2y + n2 = 0, l1x + m1y + n1' = 0 and l2x + m2y + n2' = 0 are perpendicular, then write the value of l12 − l22 + m12 − m22.
Find the locus of the mid-points of the portion of the line x sinθ+ y cosθ = p intercepted between the axes.
If a + b + c = 0, then the family of lines 3ax + by + 2c = 0 pass through fixed point
Find the equations of the lines through the point of intersection of the lines x – y + 1 = 0 and 2x – 3y + 5 = 0 and whose distance from the point (3, 2) is `7/5`
The equation of the line passing through the point (1, 2) and perpendicular to the line x + y + 1 = 0 is ______.
Equation of the line passing through the point (a cos3θ, a sin3θ) and perpendicular to the line x sec θ + y cosec θ = a is x cos θ – y sin θ = a sin 2θ.
The equation of the line joining the point (3, 5) to the point of intersection of the lines 4x + y – 1 = 0 and 7x – 3y – 35 = 0 is equidistant from the points (0, 0) and (8, 34).
The lines ax + 2y + 1 = 0, bx + 3y + 1 = 0 and cx + 4y + 1 = 0 are concurrent if a, b, c are in G.P.
