Advertisements
Advertisements
प्रश्न
Find the area of the region bounded by y = tan x, y = cot x and the lines x = 0, x = `pi/2`, y = 0
उत्तर
First find the intersecting point of y = tan x and y = cot x
tan x = cot x
`tanx/cotx` = 1
tan2x = 1
tan x = 1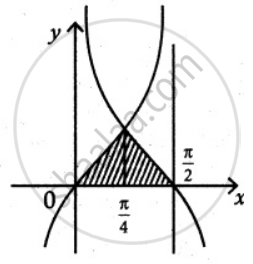
x = `pi/4`, y = 1
Required Area = `int_0^(pi/2) tan x "d"x + int_(pi/4)^(pi/2) cot x "d"x`
= `[log sec x]_0^(pi/4) + [log sin x]_(pi/4)^(pi/2)`
= `[log sec pi/4 - log sec 0] + log sin pi/2 - log sin pi/4]`
= `log sqrt(2) - 0 + 0 - log 1/sqrt(2)`
= `log sqrt(2) + log sqrt(2)`
= `2 log sqrt(2)`
= `log(sqrt2)^2`
= log 2 sq.units
APPEARS IN
संबंधित प्रश्न
Find the area of the region bounded by 3x – 2y + 6 = 0, x = – 3, x = 1 and x-axis
Find the area of the region bounded by 2x – y + 1 = 0, y = – 1, y = 3 and y-axis
Find the area of the region bounded by the curve 2 + x – x2 + y = 0, x axis, x = – 3 and x = 3
Find the area of the region bounded by the line y = 2x + 5 and the parabola y = x2 – 2x
Find the area of the region bounded between the curves y = sin x and y = cos x and the lines x = 0 and x = π
Find the area of the region bounded by the parabola y2 = x and the line y = x – 2
Father of a family wishes to divide his square field bounded by x = 0, x = 4, y = 4 and y = 0 along the curve y2 = 4x and x2 = 4y into three equal parts for his wife, daughter and son. Is it possible to divide? If so, find the area to be divided among them
The curve y = (x – 2)2 + 1 has a minimum point at P. A point Q on the curve is such that the slope of PQ is 2. Find the area bounded by the curve and the chord PQ
Find the area of the region common to the circle x2 + y2 = 16 and the parabola y2 = 6x
Choose the correct alternative:
The area between y2 = 4x and its latus rectum is
Choose the correct alternative:
If `int_0^"a" 1/(4 + x^2) "dx=pi/8` then a is
