Question

Find the area of the region common to the circle x² + y² = 16 and the parabola y² = 6x

Answer 1

First find the intersecting point of the curves

x² + y² = 16 and y² = 6x

x² + 6x = 16

x² + 6x – 16 = 0

(x + 8)(x – 2) = 0

x = – 8, x = 2

x = – 8 is impossible

x = 2, y = `2sqrt(3)`

Radius of the circle x² + y² = 16 is 4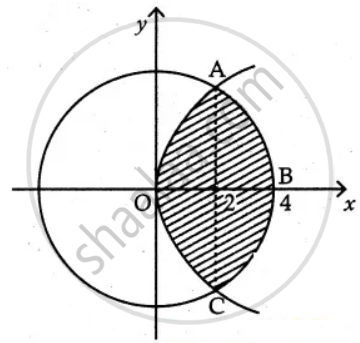

Area OABC = 2(Area of OAB)

= 2(Area of the curve y² = 6x in [0, 2] + Area of the curve x² + y² = 16 in [2, 4])

Area required = `2[int_0^2 sqrt(6x)  "d"x + int_2^4 sqrt(16  x^2)  "d"x]`

= `2([sqrt(6) x^(3/2)/(3/2)]_0^2 + [x/2 sqrt(16 - x^2) + 16/2 sin^-1  x/4]_2^4)`

= `2([2/3 sqrt(6) xx 2sqrt(2]  [(8pi)/2  sqrt(12 ) - (8pi)/6])`

= `2[4/3 sqrt(12) + (8pi)/3 - sqrt(12)]`

= `2[sqrt(12)/3 + (8pi)/3]`

=`2[(2sqrt(3))/3 + (8pi)/3]`

= `4/3 [4pi + sqrt(3)]`

Requied Area = `4/3[4pi + sqrt(3)]` sq.units