Question

The curve y = (x – 2)² + 1 has a minimum point at P. A point Q on the curve is such that the slope of PQ is 2. Find the area bounded by the curve and the chord PQ

Answer 1

y = (x – 2)² + 1 

`("d"y)/("d"x) = 2(x - 2)`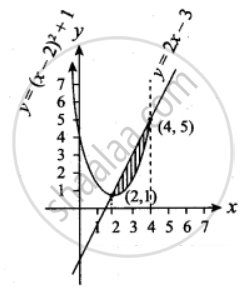

`("d"^2y)/("d"x^2)` = 2

Put `("d"y)/("d"x)` = 0, we get x = 2

At x = `2 ("d"^2y)/("d"x^2) > 0`

∴ x = 2 is a minimum point

∴ The point P is (2, 1)

But slope of PQ is 2

∴ Equation of the chord PQ

y – y₁ = m(x – x₁)

y – 1 = 2(x – 2)

y – 1 = 2x – 4

y = 2x – 3

On solving the curve and line we get the point Q(4, 5)

Requied Area =`int_2^4 (f(x) - "g"(x))  "d"x`

= `int_2^4 (2x - 3 - [(x - 2)^2 +1])  "d"x`

= `int_2^4 (6x - x^2 - 8)  "d"x`

= `[(6x^2)/2 -x^3/3 - 8x]_2^4`

= `[48 - 64/3 - 32] - [12 - 8/3 - 16]`

= `20 - 56/3`

= `4/3` sq.units