Advertisements
Advertisements
प्रश्न
Find the area of the triangle formed by the points
(1, – 1), (– 4, 6) and (– 3, – 5)
उत्तर
Let the vertices A(1, – 1), B(– 4, 6) and C(– 3, – 5)
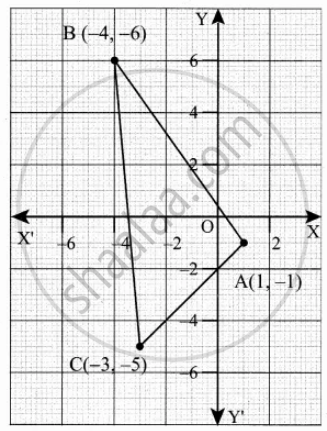
Area of ∆ABC = `1/2 [(x_1y_2 + x_2y_3 + x_3y_1) - (x_2y_1 + x_3y_2 + x_1y_3)]`
= `1/2[((-4 xx - 5) + (-3 xx - 1) + (1 xx 6)),(-(-3 xx 6) + (1 xx -5) + (- 4 xx - 1))]`
= `1/2[(6 + 20 + 3) - (4 - 18 - 5)]`
= `1/2[29 - (- 19)]`
= `1/2[29 + 19]`
= `1/2 xx 48`
= 24 sq. units
Area of ∆ABC = 24 sq. units
APPEARS IN
संबंधित प्रश्न
Sides of a triangle are in the ratio of 12 : 17 : 25 and its perimeter is 540 cm. Find its area.
The perimeter of a triangle is 300 m. If its sides are in the ratio 3 : 5 : 7. Find the area of the triangle ?
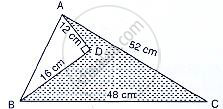
Find the area of the shaded region in the given figure.
Find the area of a quadrilateral ABCD in which AB = 42 cm, BC = 21 cm, CD = 29 cm, DA =34 cm and diagonal BD =20 cm.
Find the area of a triangle whose sides are 3 cm, 4 cm and 5 cm respectively.
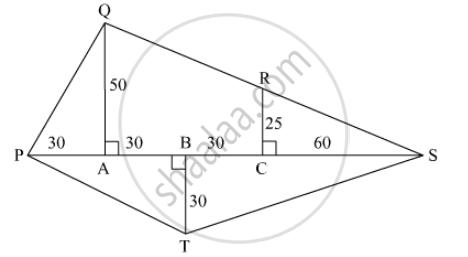
Find the areas of the given plot. (All measures are in metres.)
Find the area of triangle AGF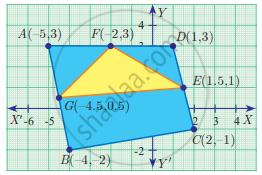
If (5, 7), (3, p) and (6, 6) are collinear, then the value of p is
The perimeter of an equilateral triangle is 30 cm. The area is
The perimeter of a triangular field is 420 m and its sides are in the ratio 6 : 7 : 8. Find the area of the triangular field.
