Advertisements
Advertisements
प्रश्न
Find the equation of the parabola in the cases given below:
End points of latus rectum (4, – 8) and (4, 8)
उत्तर
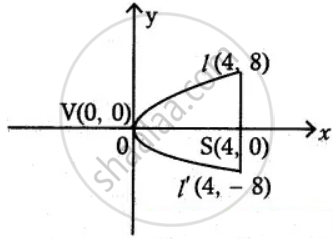
Focus = (4, 0)
Equation of the parabola will be of the form y2 = 4ax
Here a = 4
⇒ y2 = 16x
APPEARS IN
संबंधित प्रश्न
Find the equation of the parabola whose focus is the point F(-1, -2) and the directrix is the line 4x – 3y + 2 = 0.
The parabola y2 = kx passes through the point (4, -2). Find its latus rectum and focus.
Find the vertex, focus, axis, directrix, and the length of the latus rectum of the parabola y2 – 8y – 8x + 24 = 0.
Find the co-ordinates of the focus, vertex, equation of the directrix, axis and the length of latus rectum of the parabola
x2 = 8y
Find the co-ordinates of the focus, vertex, equation of the directrix, axis and the length of latus rectum of the parabola
x2 = - 16y
Find the axis, vertex, focus, equation of directrix and the length of latus rectum of the parabola (y - 2)2 = 4(x - 1)
The focus of the parabola x2 = 16y is:
The eccentricity of the parabola is:
Find the equation of the parabola in the cases given below:
Focus (4, 0) and directrix x = – 4
Find the equation of the parabola in the cases given below:
Passes through (2, – 3) and symmetric about y-axis
Find the equation of the ellipse in the cases given below:
Length of latus rectum 8, eccentricity = `3/5` centre (0, 0) and major axis on x-axis
Find the equation of the ellipse in the cases given below:
Length of latus rectum 4, distance between foci `4sqrt(2)`, centre (0, 0) and major axis as y-axis
Find the equation of the hyperbola in the cases given below:
Centre (2, 1), one of the foci (8, 1) and corresponding directrix x = 4
Find the vertex, focus, equation of directrix and length of the latus rectum of the following:
y2 = 16x
Find the vertex, focus, equation of directrix and length of the latus rectum of the following:
x2 = 24y
Find the vertex, focus, equation of directrix and length of the latus rectum of the following:
y2 = – 8x
Identify the type of conic and find centre, foci, vertices, and directrices of the following:
`x^2/3 + y^2/10` = 1
Identify the type of conic and find centre, foci, vertices, and directrices of the following:
`(x - 3)^2/225 + (y - 4)^2/289` = 1
Identify the type of conic and find centre, foci, vertices, and directrices of the following:
`(y - 2)^3/25 + (x + 1)^2/16` = 1
