Advertisements
Advertisements
Question
Find the equation of the parabola in the cases given below:
End points of latus rectum (4, – 8) and (4, 8)
Solution
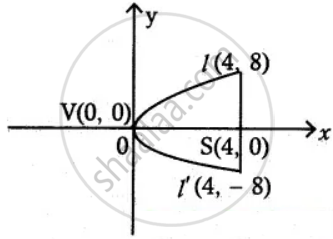
Focus = (4, 0)
Equation of the parabola will be of the form y2 = 4ax
Here a = 4
⇒ y2 = 16x
APPEARS IN
RELATED QUESTIONS
Find the equation of the parabola whose focus is the point F(-1, -2) and the directrix is the line 4x – 3y + 2 = 0.
The profit ₹ y accumulated in thousand in x months is given by y = -x2 + 10x – 15. Find the best time to end the project.
Find the equation of the parabola which is symmetrical about x-axis and passing through (–2, –3).
Find the axis, vertex, focus, equation of directrix and the length of latus rectum of the parabola (y - 2)2 = 4(x - 1)
The focus of the parabola x2 = 16y is:
The double ordinate passing through the focus is:
Find the equation of the parabola in the cases given below:
Vertex (1, – 2) and Focus (4, – 2)
Find the equation of the ellipse in the cases given below:
Foci (0, ±4) and end points of major axis are (0, ±5)
Find the equation of the hyperbola in the cases given below:
Foci (± 2, 0), Eccentricity = `3/2`
Find the vertex, focus, equation of directrix and length of the latus rectum of the following:
y2 = 16x
Find the vertex, focus, equation of directrix and length of the latus rectum of the following:
y2 = – 8x
Find the vertex, focus, equation of directrix and length of the latus rectum of the following:
x2 – 2x + 8y + 17 = 0
Find the vertex, focus, equation of directrix and length of the latus rectum of the following:
y2 – 4y – 8x + 12 = 0
Identify the type of conic and find centre, foci, vertices, and directrices of the following:
`x^2/25 + y^2/9` = 1
Identify the type of conic and find centre, foci, vertices, and directrices of the following:
`x^2/25 - y^2/144` = 1
Identify the type of conic and find centre, foci, vertices, and directrices of the following:
`(x + 1)^2/100 + (y - 2)^2/64` = 1
Identify the type of conic and find centre, foci, vertices, and directrices of the following:
`(x + 3)^2/225 + (y - 4)^2/64` = 1
