Advertisements
Advertisements
प्रश्न
For what value of `alpha` is this function `f(x) = {{:((x^4 - 1)/(x - 1)",", "if" x ≠ 1),(alpha",", "if" x = 1):}` continuous at x = 1?
उत्तर
`f(x) = {{:((x^4 - 1)/(x - 1)",", "if" x ≠ 1),(alpha",", "if" x = 1):}`
Given that f(x) is continuous at x = 1.
∴ `lim_(x -> 1) f(x) = f(1)` .......(1)
`lim_(x -> 1^-) f(x) = lim_(x -> 1^-) (x^4 - 1)/(x - 1)`
= `lim_(x -> 1^-) ((x^2 - 1)(x^2 + 1))/(x - 1)`
= `lim_(x -> 1^-) ((x + 1)(x - 1)(x^2 + 1))/(x - 1)`
= `lim_(x -> 1^-) (x + 1)(x^2 + 1)`
= `(1 + 1)(1^2 + 1)`
`lim_(x -> 1^-) f(x)` = 2 × 2 = 4 .......(2)
`lim_(x -> 1^+) f(x) = lim_(x -> 1^+) (x^4 - 1)/(x - 1)`
= `lim_(x -> 1^+) ((x^2 - 1)(x^2 + 1))/(x - 1)`
= `lim_(x -> 1^+) ((x + 1)(x - 1)(x^2 + 1))/(x - 1)`
= `lim_(x -> 1^+) (x + 1)(x^2 + 1)`
= `(1 + 1)(1^2 + 1)`
`lim_(x -> 1^-) f(x)` = 2 × 2 = 4 .......(3)
From equations (2) and (3) we have
`lim_(x -> 1^-) f(x) = lim_(x -> 1^-) f(x)` = 4
∴ `lim_(x -> 1) f(x)` = 4
`f(1) = alpha`
∴ Equation (1) ⇒ 4 = `alpha`
APPEARS IN
संबंधित प्रश्न
Prove that f(x) = 2x2 + 3x - 5 is continuous at all points in R
Examine the continuity of the following:
x + sin x
Examine the continuity of the following:
ex tan x
Examine the continuity of the following:
`(x^2 - 16)/(x + 4)`
Examine the continuity of the following:
|x + 2| + |x – 1|
Examine the continuity of the following:
`|x - 2|/|x + 1|`
Examine the continuity of the following:
cot x + tan x
Find the points of discontinuity of the function f, where `f(x) = {{:(x + 2",", "if", x ≥ 2),(x^2",", "if", x < 2):}`
Find the points of discontinuity of the function f, where `f(x) = {{:(x^3 - 3",", "if" x ≤ 2),(x^2 + 1",", "if" x < 2):}`
At the given point x0 discover whether the given function is continuous or discontinuous citing the reasons for your answer:
x0 = 1, `f(x) = {{:((x^2 - 1)/(x - 1)",", x ≠ 1),(2",", x = 1):}`
Show that the function `{{:((x^3 - 1)/(x - 1)",", "if" x ≠ 1),(3",", "if" x = 1):}` is continuous om `(- oo, oo)`
Let `f(x) = {{:(0",", "if" x < 0),(x^2",", "if" 0 ≤ x ≤ 2),(4",", "if" x ≥ 2):}`. Graph the function. Show that f(x) continuous on `(- oo, oo)`
Find the points at which f is discontinuous. At which of these points f is continuous from the right, from the left, or neither? Sketch the graph of f.
`f(x) = {{:((x - 1)^3",", "if" x < 0),((x + 1)^3",", "if" x ≥ 0):}`
Which of the following functions f has a removable discontinuity at x = x0? If the discontinuity is removable, find a function g that agrees with f for x ≠ x0 and is continuous on R.
`f(x) = (x^3 + 64)/(x + 4), x_0` = – 4
Find the constant b that makes g continuous on `(- oo, oo)`.
`g(x) = {{:(x^2 - "b"^2,"if" x < 4),("b"x + 20, "if" x ≥ 4):}`
State how continuity is destroyed at x = x0 for the following graphs.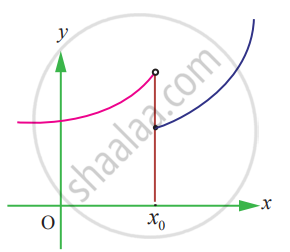
Choose the correct alternative:
If f : R → R is defined by `f(x) = [x - 3] + |x - 4|` for x ∈ R then `lim_(x -> 3^-) f(x)` is equal to
