Advertisements
Advertisements
प्रश्न
Form the differential equation of the family of ellipses having foci on y-axis and centre at origin.
उत्तर
The equation of the family of ellipses having foci on the y-axis and the centre at origin is as follows:
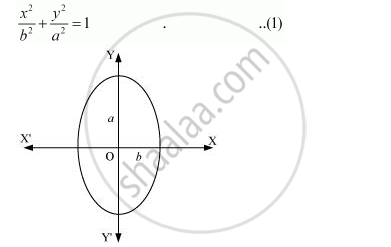

This is the required differential equation.
APPEARS IN
संबंधित प्रश्न
Form the differential equation of the family of circles having centre on y-axis and radius 3 units.
For the curve y = 5x – 2x3, if x increases at the rate of 2 units/sec, then find the rate of change of the slope of the curve when x = 3
Show that the family of curves for which `dy/dx = (x^2+y^2)/(2x^2)` is given by x2 - y2 = cx
Form the differential equation corresponding to y = emx by eliminating m.
Form the differential equation from the following primitive where constants are arbitrary:
y2 = 4ax
Form the differential equation from the following primitive where constants are arbitrary:
y = ax2 + bx + c
Find the differential equation of the family of curves y = Ae2x + Be−2x, where A and B are arbitrary constants.
Form the differential equation corresponding to (x − a)2 + (y − b)2 = r2 by eliminating a and b.
Form the differential equation of the family of curves represented by the equation (a being the parameter):
(x − a)2 + 2y2 = a2
Represent the following families of curves by forming the corresponding differential equations (a, b being parameters):
x2 − y2 = a2
Represent the following families of curves by forming the corresponding differential equations (a, b being parameters):
y2 = 4ax
Represent the following families of curves by forming the corresponding differential equations (a, b being parameters):
Represent the following families of curves by forming the corresponding differential equations (a, b being parameters):
y2 = 4a (x − b)
Represent the following families of curves by forming the corresponding differential equations (a, b being parameters):
y = eax
For the differential equation xy \[\frac{dy}{dx}\] = (x + 2) (y + 2). Find the solution curve passing through the point (1, −1).
Find one-parameter families of solution curves of the following differential equation:-
\[\frac{dy}{dx} \cos^2 x = \tan x - y\]
Find one-parameter families of solution curves of the following differential equation:-
\[e^{- y} \sec^2 y dy = dx + x dy\]
Write the differential equation representing family of curves y = mx, where m is arbitrary constant.
The differential equation which represents the family of curves y = eCx is
Form the differential equation representing the family of curves y = mx, where m is an arbitrary constant.
Find the area of the region bounded by the curves (x -1)2 + y2 = 1 and x2 + y2 = 1, using integration.
Form the differential equation representing the family of curves y = e2x (a + bx), where 'a' and 'b' are arbitrary constants.
Form the differential equation representing the family of curves y = A sin x, by eliminating the arbitrary constant A.
Find the differential equation of the family of curves y = Ae2x + B.e–2x.
Find the differential equation of the family of lines through the origin.
The differential equation representing the family of curves y = A sinx + B cosx is ______.
Find the differential equation of system of concentric circles with centre (1, 2).
Find the equation of a curve passing through (2, 1) if the slope of the tangent to the curve at any point (x, y) is `(x^2 + y^2)/(2xy)`.
Find the equation of the curve through the point (1, 0) if the slope of the tangent to the curve at any point (x, y) is `(y - 1)/(x^2 + x)`
The differential equation `y ("d"y)/("d"x) + "c"` represents: ______.
The differential equation of the family of curves x2 + y2 – 2ay = 0, where a is arbitrary constant, is ______.
Family y = Ax + A3 of curves will correspond to a differential equation of order ______.
The curve for which the slope of the tangent at any point is equal to the ratio of the abcissa to the ordinate of the point is ______.
Find the equation of the curve at every point of which the tangent line has a slope of 2x:
The area above the x-axis and under the curve `y = sqrt(1/x - 1)` for `1/2 ≤ x ≤ 1` is:
