Advertisements
Advertisements
प्रश्न
From a solid right circular cylinder of height 2.4 cm and radius 0.7 cm, a right circular cone of same height and same radius is cut out. Find the total surface area of the remaining solid.
उत्तर
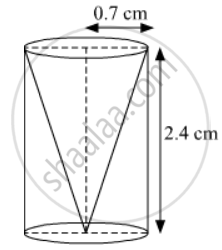
Given that,
Height (h) of the conical part = Height (h) of the cylindrical part = 2.4 cm
Radius (r) of the cylindrical part = 0.7 cm
Slant height (l) of conical part = `sqrt(r^2 + h^2)`
= `sqrt((0.7)^2 + (2.4)^2) = sqrt(0.49 + 5.76)`
`= sqrt(6.25) = 2.5`
Total surfece area of the remaining soild will be
= CSA of cylindrical part + CSA of conical part + Area of cylindrical base
`= 2pirh + pirl + pir^2`
`= 2 xx 22/7 xx 0.7 xx 2.4 + 22/7 xx 0.7 xx 2.5 + 22/7 xx 0.7 xx 0.7`
= 4.4 x 2.4 + 2.2 xx 2.5 + 2.2 xx 0.7
= 10.56 + 5.50 + 1.54 = 17.60 cm2
The total surface area of the remaining solid is 17.60 cm2
APPEARS IN
संबंधित प्रश्न
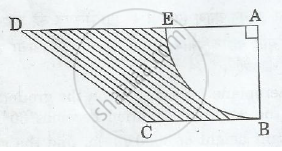
In Figure 2, ABCD is a trapezium of area 24.5 sq. cm. In it, AD|| BC, ∠ DAB = 900, AD = 10 cm and BC = 4 cm. If ABE is a quadrant of a circle, find the area of the shaded region. [Take π=22/7]
In Fig. 4, from the top of a solid cone of height 12 cm and base radius 6 cm, a cone of height 4 cm is removed by a plane parallel to the base. Find the total surface area of the remaining solid. (Use `pi=22/7` and `sqrt5=2.236`)

A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel. [Use `pi = 22/7`]
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The radius and height of the cylindrical part are 5 cm and 13 cm respectively.The radii of the hemispherical and conical parts are the same as that of the cylindrical part.Find the surface area of the toy if the total height of the toy is 30 cm.
A bucket made of aluminum sheet is of height 20cm and its upper and lower ends are of radius 25cm an 10cm, find cost of making bucket if the aluminum sheet costs Rs 70 per
100 cm2
A metallic cylinder has radius 3 cm and height 5 cm. To reduce its weight, a conical hole is drilled in the cylinder. The conical hole has a radius of `3/2` cm and its depth is `8/9 `cm. Calculate the ratio of the volume of metal left in the cylinder to the volume of metal taken out in conical shape.
The inner and outer radii of a hollow cylinder are 15 cm and 20 cm, respectively. The cylinder is melted and recast into a solid cylinder of the same height. Find the radius of the base of new cylinder.
Find the volume of a solid in the form of a right circular cylinder with hemi-spherical ends whose total length is 2.7 m and the diameter of each hemi-spherical end is 0.7 m.
Two cubes each of volume 27 cm3 are joined end to end to form a solid. Find the surface area of the resulting cuboid.
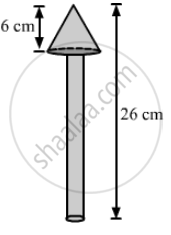
A wooden toy is in the shape of a cone mounted on a cylinder, as shown in the figure. The total height of the toy is 26 cm, while the height of the conical part is 6 cm. The diameter of the base of the conical part is 5 cm and that of the cylindrical part is 4 cm. The conical part and the cylindrical part are respectively painted red and white. Find the area to be painted by each of these colours. `["Take" pi = 22/7]`