Advertisements
Advertisements
प्रश्न
हल कीजिए: -12x > 30, जब x एक प्राकृत संख्या है।
उत्तर
दी गई असमिका -12x > 30 है।
- 12x > 30
⇒ `(-12x)/(-12) < 30/(-12)` (दोनों पक्षों को एक ही ऋणात्मक संख्या से विभाजित करने पर)
⇒ x < `- 5/2`
(-5/2) से कम कोई प्राकृत संख्या नहीं है।
इस प्रकार, जब x एक प्राकृत संख्या है, तो दी गई असमिका का कोई हल नहीं है।
APPEARS IN
संबंधित प्रश्न
हल कीजिए: 24x < 100, जब x एक प्राकृत संख्या है।
हल कीजिए 24x < 100, जब x एक पूर्णांक है।
हल कीजिए: -12x > 30, जब x एक पूर्णांक है।
हल कीजिए: 5x – 3 <7, जब x एक वास्तविक संख्या है।
हल कीजिए: 3x + 8 > 2, जब x एक पूर्णांक है।
निम्नलिखित प्रश्न वास्तविक संख्या x के लिए हल कीजिए: 4x + 3 < 6x + 7
निम्नलिखित प्रश्न वास्तविक संख्या x के लिए हल कीजिए: 3x – 7 > 5x – 1
निम्नलिखित प्रश्न वास्तविक संख्या x के लिए हल कीजिए: 3(x – 1) ≤ 2 (x – 3)
निम्नलिखित प्रश्न वास्तविक संख्या x के लिए हल कीजिए: 3(2 – x) ≥ 2 (1 – x)
निम्नलिखित प्रश्न वास्तविक संख्या x के लिए हल कीजिए: ` x +x/2` + `x/3` <11
निम्नलिखित प्रश्न वास्तविक संख्या x के लिए हल कीजिए: `x/3 > x/2 + 1`
निम्नलिखित प्रश्न वास्तविक संख्या x के लिए हल कीजिए: `1/2 ((3x)/5 + 4) >= 1/3 (x -6)`
निम्नलिखित प्रश्न वास्तविक संख्या x के लिए हल कीजिए: 37 – (3x + 5) ≥ 9x – 8(x – 3)
दी गई असमिका का हल ज्ञात कीजिए तथा संख्या रेखा पर आलेखित कीजिए।
`x/2 >= (5x -2)/3 - (7x - 3)/5`
रवि ने पहली दो एकक परीक्षा में 70 और 75 अंक प्राप्त किए हैं। वह न्यूनतम अंक ज्ञात कीजिए, जिसे वह तीसरी एकक परीक्षा में पाकर 60 अंक का न्यूनतम औसत प्राप्त कर सके।
किसी पाठ्यक्रम में ग्रेड 'A' पाने के लिए एक व्यक्ति को सभी पाँच परीक्षाओं (प्रत्येक 100 अंकों में से) में 90 अंक या अधिक अंक का औसत प्राप्त करना चाहिए यदि सुनीता के प्रथम चार परीक्षाओं के प्राप्तांक 87,92, 94 और 95 हों तो वह न्यूनतम अंक ज्ञात कीजिए जिसे पांचवीं परीक्षा में प्राप्त करके सुनीता उस पाठ्यक्रम में ग्रेड 'A' पाएगी।
असमानता को हल कीजिए:
2 ≤ 3x – 4 ≤ 5
असमिका को हल कीजिए:
`-12 < 4 - (3x)/(-5) <= 2`
असमानता को हल कीजिए:
`7 <= (3x + 11)/2 <= 11`
असमिकाओं को हल कीजिए और हल को संख्या रेखा पर निरूपित कीजिए।
3x – 7 > 2(x -6), 6 – x > 11 – 2x
असमिकाओं को हल कीजिए और हल को संख्या रेखा पर निरूपित कीजिए।
5(2x – 7) – 3(2x + 3) ≤ 0, 2x + 19 ≤ 6x + 47
ऐसी रैखिक असमिकाएँ ज्ञात कीजिए जिनका हल समुच्चय नीचे प्रदर्शित आकृति का छायांकित भाग है।
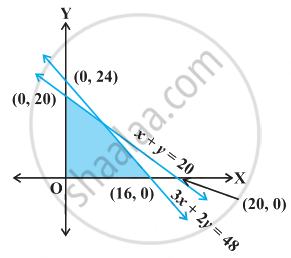
प्रश्न में x चर वाले किसी रैखिक असमिका के हल को संख्या रेखा पर निरूपित किया गया है।

प्रश्न में x चर वाले किसी रैखिक असमिका के हल को संख्या रेखा पर निरूपित किया गया है।
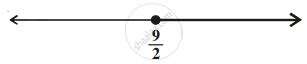
प्रश्न में x चर वाले किसी रैखिक असमिका के हल को संख्या रेखा पर निरूपित किया गया है।

