Advertisements
Advertisements
प्रश्न
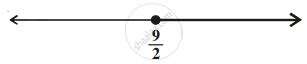
प्रश्न में x चर वाले किसी रैखिक असमिका के हल को संख्या रेखा पर निरूपित किया गया है।

विकल्प
x ∈ (–∞, –2)
x ∈ (–∞, –2]
x ∈ (–2, ∞]
x ∈ [–2, ∞)
उत्तर
x ∈ (–∞, –2]
स्पष्टीकरण:
इस पर गौर करें कि, ग्राफ़ x के सभी वास्तविक मानों से कम और −2 के बराबर का प्रतिनिधित्व करता है।
इसलिए, x ∈ (−∞, −2]
सही उत्तर x ∈ (−∞, −2] है।
APPEARS IN
संबंधित प्रश्न
हल कीजिए: 24x < 100, जब x एक प्राकृत संख्या है।
हल कीजिए: -12x > 30, जब x एक पूर्णांक है।
हल कीजिए: 3x + 8 > 2, जब x एक वास्तविक संख्या है।
निम्नलिखित प्रश्न वास्तविक संख्या x के लिए हल कीजिए: 3x – 7 > 5x – 1
निम्नलिखित प्रश्न वास्तविक संख्या x के लिए हल कीजिए: 3(x – 1) ≤ 2 (x – 3)
निम्नलिखित प्रश्न वास्तविक संख्या x के लिए हल कीजिए: 3(2 – x) ≥ 2 (1 – x)
निम्नलिखित प्रश्न वास्तविक संख्या x के लिए हल कीजिए: `x/3 > x/2 + 1`
निम्नलिखित प्रश्न वास्तविक संख्या x के लिए हल कीजिए: `(3(x-2))/5 <= (5(2-x))/3`
निम्नलिखित प्रश्न वास्तविक संख्या x के लिए हल कीजिए: `1/2 ((3x)/5 + 4) >= 1/3 (x -6)`
निम्नलिखित प्रश्न वास्तविक संख्या x के लिए हल कीजिए: 2(2x + 3) – 10 < 6 (x – 2)
निम्नलिखित प्रश्न वास्तविक संख्या x के लिए हल कीजिए: `((2x- 1))/3 >= ((3x - 2))/4 - ((2-x))/5`
दी गई असमिका का हल ज्ञात कीजिए तथा संख्या रेखा पर आलेखित कीजिए।
3(1 – x) < 2 (x + 4)
10 से कम क्रमागत विषम संख्याओं के ऐसे युग्म ज्ञात कीजिए जिनके योगफल 11 से अधिक हों।
क्रमागत सम संख्याओं के ऐसे युग्म ज्ञात कीजिए जिनमें से प्रत्येक 5 से बड़े हों, तथा उनका योगफल 23 से कम हो।
एक व्यक्ति 91 सेमी लंबे बोर्ड में से तीन लंबाईयाँ काटना चाहता है। दूसरी लंबाई सबसे छोटो लंबाई से 3 सेमी अधिक और तीसरी लंबाई सबसे छोटी लंबाई की दूनी है। सबसे छोटे बोर्ड की संभावित लंबाई क्या है, यदि तीसरा टुकड़ा दूसरे टुकड़े से कम से कम 5 सेमी अधिक लंबा हो?
[संकेत: यदि सबसे छोटे बोर्ड की लंबाई x सेमी हो, तब (x + 3 ) सेमी और 2x सेमी क्रमश: दूसरे और तीसरे टुकड़ों की लंबाईयाँ हैं। इस प्रकार x + (x + 3) + 2x ≤ 91 और 2x ≥ (x + 3 ) + 5]
असमानता को हल कीजिए:
2 ≤ 3x – 4 ≤ 5
असमानता को हल कीजिए:
6 ≤ – 3 (2x – 4) < 12
असमानता को हल कीजिए:
- 3 ≤ 4 - `(7x)/2 ≤ 18`
असमानता को हल कीजिए:
`-15 < (3(x - 2))/5 <= 0`
असमिकाओं को हल कीजिए और हल को संख्या रेखा पर निरूपित कीजिए।
3x – 7 > 2(x -6), 6 – x > 11 – 2x
असमिकाओं को हल कीजिए और हल को संख्या रेखा पर निरूपित कीजिए।
5(2x – 7) – 3(2x + 3) ≤ 0, 2x + 19 ≤ 6x + 47
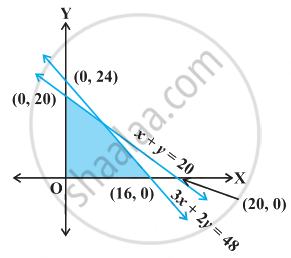
ऐसी रैखिक असमिकाएँ ज्ञात कीजिए जिनका हल समुच्चय नीचे प्रदर्शित आकृति का छायांकित भाग है।
प्रश्न में x चर वाले किसी रैखिक असमिका के हल को संख्या रेखा पर निरूपित किया गया है।