Advertisements
Advertisements
प्रश्न
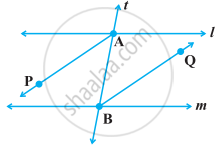
In the following figure, bisectors AP and BQ of the alternate interior angles are parallel, then show that l ||m.
उत्तर
Given, In the following figure AP || BQ, AP and BQ are the bisectors of alternate interior angles ∠CAB and ∠ABF.
To show l || m
Proof Since, AP || BQ and t is transversal, therefore ∠PAB = ∠ABQ ...[Alternate interior angles]
⇒ 2∠PAB = 2∠ABQ ...[Multiplying both sides by 2]
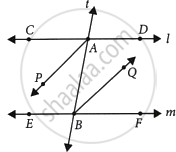
∠CAB = ∠ABF
So, alternate interior angles are equal.
We know that, if two alternate interior angles are equal, then lines are parallel.
Hence, l || m.
APPEARS IN
संबंधित प्रश्न
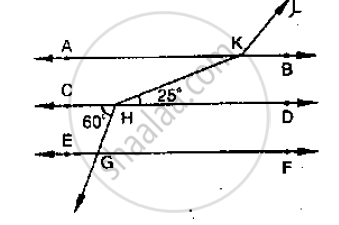
In the below fig, AB || CD || EF and GH || KL. Find `∠`HKL
In the below fig, lines AB and CD are parallel and P is any point as shown in the figure.
Show that` ∠`ABP +` ∠`CDP = ∠DPB.
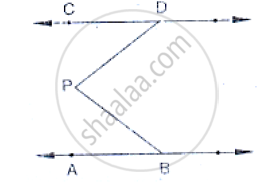
Prove that the straight lines perpendicular to the same straight line are parallel to one
another.
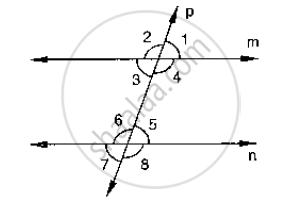
In the below fig, p is a transversal to lines m and n,`∠`2 = 120° and `a∠`5 = 60°. Prove that m || n.
Fill in the blank in the following to make the statement true:
If two parallel lines are intersected by a transversal, then interior angles on the same
side of the transversal are _______
Fill in the blank :
If a transversal intersects a pair of lines in such a way that the sum of interior angles
on the same side of transversal is 180°, then the lines are _______.
In the given figure, if AB || CD, then x =

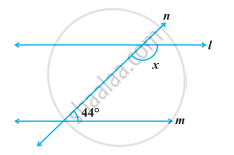
In the given figure, if l || m, then x =

In the following figure, if OP || RS, ∠OPQ = 110° and ∠QRS = 130°, then ∠PQR is equal to ______.

In the following figure, find the value of x for which the lines l and m are parallel.