Advertisements
Advertisements
प्रश्न
किसी मोबाइल फोन पर किये गये कॉलों के समय-काल का बारंबारता बंटन नीचे दिया गया है:
|
समय काल (सेकंडों में) |
कॉलों की संख्या |
| 95 – 125 | 14 |
| 125 – 155 | 22 |
| 155 – 185 | 28 |
| 185 – 215 | 21 |
| 215 – 245 | 15 |
इन कॉलों का औसत समय काल (सेकंडों में) परिकलित कीजिए तथा साथ ही संचयी बारंबारता वक्र से माध्यक भी ज्ञात कीजिए।
उत्तर
सबसे पहले, हम निम्नानुसार वर्ग अंकों की गणना करते हैं।
|
समय काल |
कॉलो की संख्या |
वर्ग चिह्न |
`bb(u_i = (x_i - a)/h)`
|
`bb(f_iu_i)`
|
|
95 – 125 |
14 |
110 |
– 2 |
– 28 |
|
125 – 155 |
22 |
140 |
– 1 |
– 22 |
|
155 – 185 |
28 |
a = 170 |
0 |
0 |
|
185 – 215 |
21 |
200 |
1 |
21 |
|
215 – 245 |
15 |
230 |
2 |
30 |
|
|
`sumf_i = 100`
|
|
|
`sumf_iu_i = 1`
|
यहाँ, (अनुमानित माध्य) a = 170,
और (वर्ग चौड़ाई) h = 30
चरण विचलन विधि द्धारा,
औसत `(barx) = a + (sumf_iu_i)/(sumf_i) xx h`
= `170 + 1/100 xx 30`
= 170 + 0.3
= 170.3
अतः, औसत अवधि 170.3 सेकंड हैं।
संचयी आवृत्ति वक्र से माध्यिका की गणना के लिए
हम प्रकार से कम या प्रकार से अधिक तोरण तैयार करते हैं।
हमने देखा कि, 95 सेकंड से कम समय में कॉलों की संख्या 0 है। इसी प्रकार, 125 सेकंड से कम में 95 सेकंड से कम में कॉल की संख्या के साथ-साथ 95 – 125.एस से कॉल की संख्या भी शामिल है। तो, 125 सेकंड से कम कॉल की कुल संख्या 0 + 14 = 14 है। इसी तरह आगे बढ़ते रहने पर हम 155, 185, 215 और 245 सेकेंड से भी कम समय में शेष रह जाएंगे।
अब, हम तोरण (संचयी आवृत्ति वक्र) से कम के लिए एक तालिका बनाते हैं।
|
से कम प्रकार |
||
|
समय काल (सेकंड में) |
कॉलो की संख्या |
|
|
95 से कम |
0 |
|
|
125 से कम |
0 + 14 = 14 |
|
|
155 से कम |
14 + 22 = 36 |
|
|
185 से कम |
36 + 28 = 64 |
|
|
215 से कम |
64 + 21 = 85 |
|
|
245 से कम |
85 + 15 = 100 |
|
प्रकार के तोरण से कम अंक निकालने के लिए हम उन पर अंक आलेखित करते हैं (95, 0), (125, 14) (155, 36), (185, 64), (215, 85), (245, 100) कागज पर और मुक्त हाथ से उन्हें जोड़ दें।
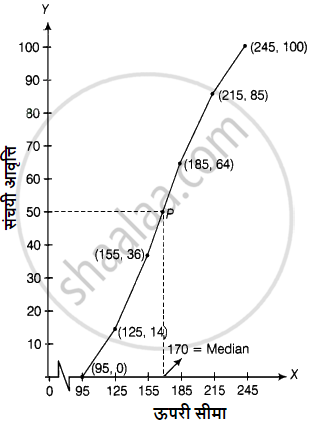
∴ कॉल की कुल संख्या (n) = 100
∴ `n/2 = 100/2 = 50`
अब, बिंदु 50 को Y-अक्ष पर लेते हुए X-अक्ष के समानांतर एक रेखा खींचें जो बिंदु P पर मिलती है और P से X-अक्ष पर एक लंबवत रेखा खींचें, X-अक्ष का प्रतिच्छेदन बिंदु माध्यिका है।
अतः, अभीष्ट माध्यिका 170 है।
APPEARS IN
संबंधित प्रश्न
निम्नलिखित वितरण एक इलाके के बच्चों के दैनिक जेब भत्ते को दर्शाता है। औसत जेब भत्ता 18 रुपये है। लापता आवृत्ति का पता लगाएं f ज्ञात कीजिए:
|
दैनिक जेब भत्ता (रुपये में) |
11-13 | 13-15 | 15-17 | 17-19 | 19-21 | 21-23 | 23-25 |
| श्रमिकों की संख्या | 7 | 6 | 9 | 13 | f | 5 | 4 |
हवा में SO2 की सांद्रता का पता लगाने के लिए (प्रति मिलियन भागों में, यानी, ppm), एक निश्चित शहर में 30 इलाकों के लिए डेटा एकत्र किया गया था और नीचे प्रस्तुत किया गया है:
| SO2 की सांद्रता (ppm में) | आवृत्ति |
| 0.00 − 0.04 | 4 |
| 0.04 − 0.08 | 9 |
| 0.08 − 0.12 | 9 |
| 0.12 − 0.16 | 2 |
| 0.16 − 0.20 | 4 |
| 0.20 − 0.24 | 2 |
हवा में SO2 की औसत सांद्रता ज्ञात कीजिए।
यदि नीचे दिए हुए बंटन का माध्यक 28.5 हो तो x और y के मान ज्ञात कीजिए:
| कक्षा अन्तराल | आवृत्ति |
| 0 - 10 | 5 |
| 10 - 20 | x |
| 20 - 30 | 20 |
| 30 - 40 | 15 |
| 40 - 50 | y |
| 50 - 60 | 5 |
| Total | 60 |
निम्नलिखित सारणी 400 नियाॅन लैंपों के जीवन कालों को प्रदर्शित करती है:
| जीवन काल (घंटों में) | लैंप की संख्या |
| 1500 – 2000 | 14 |
| 2000 – 2500 | 56 |
| 2500 – 3000 | 60 |
| 3000 – 3500 | 86 |
| 3500 – 4000 | 74 |
| 4000 – 4500 | 62 |
| 4500 – 5000 | 48 |
एक लैंप का माध्यक जीवन काल ज्ञात कीजिए।
अवर्गीकृत आँकड़ों का माध्यक और इन्हीं आँकड़ों को वर्गीकृत करने के बाद परिकलित माध्यक सदैव बराबर होते हैं। क्या आप सोचते हैं कि यह कथन सत्य है? कारण दीजिए।
निम्नलिखित बंटन के लिए, माध्य प्राप्तांक ज्ञात कीजिए:
| प्राप्तांक | विद्यार्थियों की संख्या |
| 0 और उससे अधिक | 80 |
| 10 और उससे अधिक | 77 |
| 20 और उससे अधिक | 72 |
| 30 और उससे अधिक | 65 |
| 40 और उससे अधिक | 55 |
| 50 और उससे अधिक | 43 |
| 60 और उससे अधिक | 28 |
| 70 और उससे अधिक | 16 |
| 80 और उससे अधिक | 10 |
| 90 और उससे अधिक | 8 |
| 100 और उससे अधिक | 0 |
70 पैकेटों में चाय के भार नीचे दी सारणी में दर्शाए गये हैं:
| भार (ग्राम में) | पैकेटों की संख्या |
| 200 – 201 | 13 |
| 201 – 202 | 27 |
| 202 – 203 | 18 |
| 203 – 204 | 10 |
| 204 – 205 | 1 |
| 205 – 206 | 1 |
इन आँकड़ों के लिए, 'से कम प्रकार' का तोरण खींचिए तथा इसका प्रयोग माध्यक भार ज्ञात करने में कीजए।
70 पैकेटों में चाय के भार नीचे दी सारणी में दर्शाए गये हैं:
| भार (ग्राम में) | पैकेटों की संख्या |
| 200 – 201 | 13 |
| 201 – 202 | 27 |
| 202 – 203 | 18 |
| 203 – 204 | 10 |
| 204 – 205 | 1 |
| 205 – 206 | 1 |
इन आँकड़ों के लिए, 'से कम प्रकार' और 'से अधिक प्रकार' के तोरण खींचिए तथा इनका माध्यक भार ज्ञात करने में प्रयोग कीजिए।
निम्नलिखित आँकड़ों का माध्यक 50 है। यदि सभी बारंबारताओं का योग 90 है, तो p और q के मान ज्ञात कीजिए।
| प्राप्तांक | बारंबारता |
| 20 – 30 | p |
| 30 – 40 | 15 |
| 40 – 50 | 25 |
| 50 – 60 | 20 |
| 60 – 70 | q |
| 70 – 80 | 8 |
| 80 – 90 | 10 |
किसी शहर में एक वर्ष के 66 दिन की वर्षा का रिकार्ड नीचे सारणी में दिया गया है:
|
वर्षा (cm में) |
0 – 10 |
10 – 20 |
20 – 30 |
30 – 40 |
40 – 50 |
50 – 60 |
|
दिनों की संख्या |
22 |
10 |
8 |
15 |
5 |
6 |
'से कम प्रकार' और 'से अधिक प्रकार के' तोरणों का प्रयोग करके माध्यक वर्षा परिकलित कीजिए।
