Advertisements
Advertisements
प्रश्न
निम्न समांतर चतुर्भुज में अज्ञात x, y, z के मानों को ज्ञात कीजिए :

उत्तर
x + 80° = 180° ...[आसन्न कोणों का योग 180° होता है]
x = 180° − 80° = 100°
साथ ही 80° = y ...[∵ समांतर चतुर्भुज सम्मुख कोण समान होते है]
और x = 180° − z ⇒ 100° = 180° − z
⇒ z = 180° − 100° = 80°
इस प्रकार x = 100°, y = 80° और z = 80°
APPEARS IN
संबंधित प्रश्न
दर्शाइए कि एक वर्ग के विकर्ण बराबर होते हैं और परस्पर समकोण पर समद्विभाजित करते हैं।
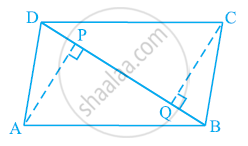
ABCD एक समांतर चतुर्भज है तथा AP और CQ शीर्षों A और C से विकर्ण BD पर क्रमशः लम्ब हैं (देखिए आकृति में)। दर्शाइए कि
- ΔAPB ≅ ΔCQD
- AP = CQ
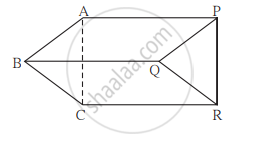
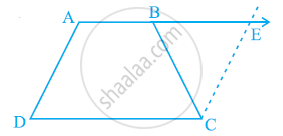
ABCD एक समलंब है, जिसमें AB || DC और AD = BC है (देखिए आकृति में)। दर्शाइए कि
- ∠A = ∠B
- ∠C = ∠D
- ΔABC ≅ ΔBAD
- विकर्ण AC = विकर्ण BD है।
[संकेत: AB को बढ़ाइए और C से होकर DA के समांतर एक रेखा खींचिए जो बढ़ी हुई भुजा AB को E पर प्रतिच्छेद करे।]
किसी समांतर चतुर्भुज के दो आसन्न कोणों का अनुपात 3 : 2 है। समांतर चतुर्भुज के सभी कोणों की माप ज्ञात कीजिए।
निम्नलिखित के लिए कारण दीजिए:
वर्ग, आयत, समांतर चतुर्भुज और समचतुर्भुज में से प्रत्येक एक चतुर्भुज भी है।
एक समांतर चतुर्भुज के विकर्ण परस्पर लंब होते हैं। क्या यह कथन सत्य है? अपने उत्तर के लिए कारण दीजिए।
चतुर्भुज ABCD में, ∠A + ∠D = 180° है। इस चतुर्भुज को कौन-सा विशेष नाम दिया जा सकता है?
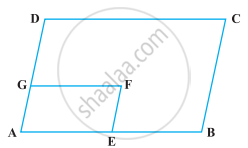
निम्नलिखित आकृति में, ABCD और AEFG दो समांतर चतुर्भुज हैं यदि ∠C = 55° है, तो ∠F निर्धारित कीजिए।
यदि किसी समांतर चतुर्भुज के दो आसन्न कोण (5x − 5)∘ और (10x + 35)∘ हैं, तो इन कोणों का अनुपात होगा –
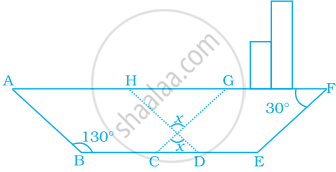
नीचे दिये गये एक जहाज कौँ आकृति में, ABDH और CEFG दो समांतर चतुर्भुज हैं। x का मान ज्ञात कीजिए।
ABCD एक समांतर चतुर्भुज है। कोण A का समद्विभाजक CD को X पर प्रतिच्छेद करता है तथा कोण C का समद्विभाजक AB को Y पर प्रतिच्छेद करता है। क्या AXCY एक समांतर चतुर्भुज है? कारण दीजिए।
समांतर ABCD में, ∠A का समद्विभाजक BC को समद्विभाजित करता है। क्या कोण B का समद्विभाजक AD को भी समद्विभाजित करता है? कारण दीजिए।
एक समांतर चतुर्भुज HOME की रचना कीजिए, जिसमें HO = 6 cm, HE = 4 cm और OE = 3 cm है।
किसी समांतर चतुर्भुज के दो संलग्न कोणों के मापों का अनुपात 1 : 2 हो तो उस समांतर चतुर्भुज के सभी कोणों के माप ज्ञात कीजिए।
आकृति में `square` ABCD समांतर चतुर्भुज है। किरण AB पर बिंदु E इस प्रकार है कि BE = AB तो सिद्ध कीजिए कि रेखा ED यह रेख BC को बिंदु F पर समद्विभाजित करती है।

संलग्न आकृति में समांतर चतुर्भुज `square` ABCD की भुजाओं पर P, Q, R, S इस प्रकार है कि, AP = BQ = CR = DS तो सिद्ध कीजिए कि `square` PQRS समांतर चतुर्भुज है।

समांतर चतुर्भुज की दो संलग्न भुजाओं का अनुपात 3 : 4 है। उसकी परिमिति 112 सेमी हो तो उसकी प्रत्येक भुजा की लंबाई ज्ञात कीजिए।
संलग्न आकृति में रेख AB || रेख PQ , रेख AB ≅ रेख PQ, रेख AC || रेख PR, रेख AC ≅ रेख PR तो सिद्ध कीजिए कि रेख BC || रेख QR तथा रेख BC ≅ रेख QR