Advertisements
Advertisements
प्रश्न
O केंद्र असलेल्या वर्तुळाची OA ही त्रिज्या आहे. जर A चे निर्देशक (0, 2) असतील तर बिंदू (1, 2) हा वर्तुळावर आहे किंवा नाही पडताळा घ्या.
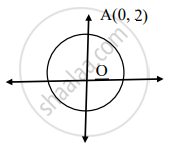
उत्तर
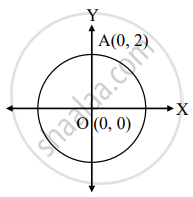
बिंदू A चे निर्देशक = (0, 2)
बिंदू O चे निर्देशक = (0, 0)
बिंदू B चे निर्देशक = (1, 2)
दोन बिंदूंमधील अंतर = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2)`
अंतराच्या सूत्रानुसार,
d(O, A) = `sqrt((0 - 0)^2 + (0 - 2)^2)`
= `sqrt((0)^2 + (-2)^2)`
= `sqrt(0 + 4)`
= 2 ................(i)
d(O, B) = `sqrt((0 - 1)^2 + (0 - 2)^2)`
= `sqrt((-1)^2 + (-2)^2)`
= `sqrt(1 + 4)`
= `sqrt5` ..............(ii)
∴ (i) आणि (ii) वरून
d(O, B) > d(O, A)
∴ d(O, B) > वर्तुळाची त्रिज्या
∴ बिंदू (1, 2) हा वर्तुळावर नाही, वर्तुळाच्या बाहेर आहे.
APPEARS IN
संबंधित प्रश्न
जर बिंदू L(x, 7) आणि M(1, 15) यातील अंतर 10 असेल, तर x ची किंमत काढा.
X-अक्षावरील असा बिंदू शोधा की जो P(2,-5) आणि Q(-2,9) पासून समदूर असेल.
खालील बिंदूंतील अंतर काढा.
R(-3a, a), S(a, -2a)
खालील बिंदूंना जोडणारे रेषाखंड त्रिकोण तयार करू शकतील का? त्रिकोण तयार झाल्यास त्याचा बाजूंवरून होणारा प्रकार सांगा.
A(`sqrt2` , `sqrt2`), B(`-sqrt2` , `-sqrt2`), C(`-sqrt6`, `sqrt6`)
C(–3a, a), D(a, –2a) या दोन बिंदूंमधील अंतर काढा.
दाखवा की, बिंदू (11, –2) हा (4, –3) आणि (6, 3) या बिंदूंपासून समदूर आहे.
(0, 9) हा बिंदू (–4, 1) व (4, 1) या बिंदूंपासून समदूर आहे हे दाखवा.
(0, –1), (8, 3), (6, 7) व (–2, 3) हे बिंदू आयताचे शिरोबिंदू आहेत हे दाखवा.
A(5, 4), B(–3, –2) आणि C(1, –8) हे ∆ABC चे शिरोबिंदू असून रेख AD मध्यगा असेल, तर रेख AD ची लांबी किती?
O(0, 0) आणि P(3, 4) या दोन बिंदूतील अंतर काढा.
