Advertisements
Advertisements
प्रश्न
The human body has an average temperature of 98°F. Assume that the vapour pressure of the blood in the veins behaves like that of pure water. Find the minimum atmospheric pressure which is necessary to prevent the blood from boiling. Use figure for the vapour pressures.

उत्तर
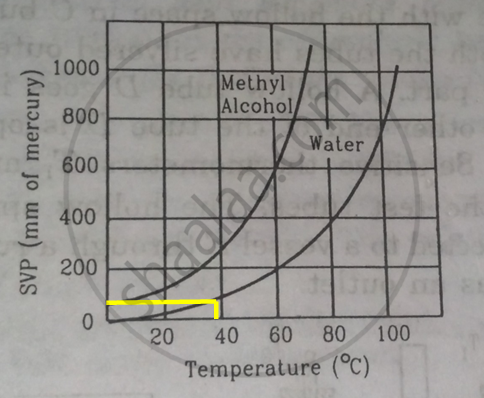
Here ,
`"T" = 98^circ "F"`
When we convert the temperature to °C , we get
`5/9("F" - 32)`
= `5/9(98 - 32)`
= `36.7^circ C`
We drop perpendicular corresponding to a temperature of 36.70C on Y-axis from the curve of pure water. This gives the boiling point of blood 50 mm of Hg.
APPEARS IN
संबंधित प्रश्न
While gas from a cooking gas cylinder is used, the pressure does not fall appreciably till the last few minutes. Why?
A gas is kept in a rigid cubical container. If a load of 10 kg is put on the top of the container, does the pressure increase?
If it were possible for a gas in a container to reach the temperature 0 K, its pressure would be zero. Would the molecules not collide with the walls? Would they not transfer momentum to the walls?
The pressure of a gas kept in an isothermal container is 200 kPa. If half the gas is removed from it, the pressure will be
Equal masses of air are sealed in two vessels, one of volume V0 and the other of volume 2V0. If the first vessel is maintained at a temperature 300 K and the other at 600 K, find the ratio of the pressures in the two vessels.
Use R = 8.31 JK-1 mol-1
2 g of hydrogen is sealed in a vessel of volume 0.02 m3 and is maintained at 300 K. Calculate the pressure in the vessel.
Use R=8.3J K-1 mol-1
Figure shows a cylindrical tube with adiabatic walls and fitted with a diathermic separator. The separator can be slid in the tube by an external mechanism. An ideal gas is injected into the two sides at equal pressures and equal temperatures. The separator remains in equilibrium at the middle. It is now slid to a position where it divides the tube in the ratio of 1:3. Find the ratio of the pressures in the two parts of the vessel.
Use R=8.314J K-1 mol-1

Air is pumped into an automobile tyre's tube up to a pressure of 200 kPa in the morning when the air temperature is 20°C. During the day the temperature rises to 40°C and the tube expands by 2%. Calculate the pressure of the air in the tube at this temperature.
An air bubble of radius 2.0 mm is formed at the bottom of a 3.3 m deep river. Calculate the radius of the bubble as it comes to the surface. Atmospheric pressure = 1.0 × 105 Pa and density of water = 1000 kg m−3.
A container of volume 50 cc contains air (mean molecular weight = 28.8 g) and is open to atmosphere where the pressure is 100 kPa. The container is kept in a bath containing melting ice (0°C). (a) Find the mass of the air in the container when thermal equilibrium is reached. (b) The container is now placed in another bath containing boiling water (100°C). Find the mass of air in the container. (c) The container is now closed and placed in the melting-ice bath. Find the pressure of the air when thermal equilibrium is reached.
Use R = 8.3 J K-1 mol-1
Is a slow process always isothermal? Is a quick process always adiabatic?
A vessel of volume V0 contains an ideal gas at pressure p0 and temperature T. Gas is continuously pumped out of this vessel at a constant volume-rate dV/dt = r keeping the temperature constant. The pressure of the gas being taken out equals the pressure inside the vessel. Find (a) the pressure of the gas as a function of time, (b) the time taken before half the original gas is pumped out.
Use R = 8.3 J K−1 mol−1
An ideal gas is kept in a long cylindrical vessel fitted with a frictionless piston of cross-sectional area 10 cm2 and weight 1 kg. The length of the gas column in the vessel is 20 cm. The atmospheric pressure is 100 kPa. The vessel is now taken into a spaceship revolving round the earth as a satellite. The air pressure in the spaceship is maintained at 100 kPa. Find the length of the gas column in the cylinder.
Use R = 8.3 J K-1 mol-1
A gas is enclosed in a cylindrical can fitted with a piston. The walls of the can and the piston are adiabatic. The initial pressure, volume and temperature of the gas are 100 kPa, 400 cm3 and 300 K, respectively. The ratio of the specific heat capacities of the gas, Cp / Cv = 1.5. Find the pressure and the temperature of the gas if it is (a) suddenly compressed (b) slowly compressed to 100 cm3.
Two glass bulbs of equal volume are connected by a narrow tube and are filled with a gas at 0°C at a pressure of 76 cm of mercury. One of the bulbs is then placed in melting ice and the other is placed in a water bath maintained at 62°C. What is the new value of the pressure inside the bulbs? The volume of the connecting tube is negligible.
A barometer tube is 80 cm long (above the mercury reservoir). It reads 76 cm on a particular day. A small amount of water is introduced in the tube and the reading drops to 75.4 cm. Find the relative humidity in the space above the mercury column if the saturation vapour pressure at the room temperature is 1.0 cm.
The temperature and humidity of air are 27°C and 50% on a particular day. Calculate the amount of vapour that should be added to 1 cubic metre of air to saturate it. The saturation vapour pressure at 27°C = 3600 Pa.
Use R = 8.3 J K-1 mol-1
Air separated from the atmosphere by a column of mercury of length h = 15 cm is present in a narrow cylindrical two-soldered at one end. When the tube is placed horizontally the air occupies a volume V1 = 240 mm3. When it is set vertically with its open end upwards the volume of the air is V2 = 200 mm3. The atmospheric pressure during the experiment is 7n cm of Hg where n is a single digit number. n will be ______.
