Advertisements
Advertisements
प्रश्न
“Politics is the art of the possible”. Similarly, “Science is the art of the soluble”. Explain this beautiful aphorism on the nature and practice of science.
उत्तर १
Science is a systematised study of observations. A scientist patiently analyses these observations and comes out with certain laws. As an illustration, Tycho Brahe worked for twenty long years to make observations on planetary motions. It is from this huge reservoir of observations that Kepler formulated his three famous laws of planetary motion. Thus, science is the art of the soluble just as politics is the art of the possible.
उत्तर २
It is well known that to win over votes, politicians would make anything and everything possible even when they are least sure of the same. and in Science the various natural phenomena can be explained in terms of some basic laws. So as 'Politics is the art of possible' similarly 'Science is the art of the soluble'.
APPEARS IN
संबंधित प्रश्न
Find the dimensions of linear momentum .
Find the dimensions of magnetic field B.
The relevant equation are \[F = qE, F = qvB, \text{ and }B = \frac{\mu_0 I}{2 \pi a};\]
where F is force, q is charge, v is speed, I is current, and a is distance.
Test if the following equation is dimensionally correct:
\[v = \sqrt{\frac{P}{\rho}},\]
where v = velocity, ρ = density, P = pressure
Test if the following equation is dimensionally correct:
\[V = \frac{\pi P r^4 t}{8 \eta l}\]
where v = frequency, P = pressure, η = coefficient of viscosity.
Let x and a stand for distance. Is
\[\int\frac{dx}{\sqrt{a^2 - x^2}} = \frac{1}{a} \sin^{- 1} \frac{a}{x}\] dimensionally correct?
Let \[\vec{A} = 5 \vec{i} - 4 \vec{j} \text { and } \vec{B} = - 7 \cdot 5 \vec{i} + 6 \vec{j}\]. Do we have \[\vec{B} = k \vec{A}\] ? Can we say \[\frac{\vec{B}}{\vec{A}}\] = k ?
A situation may be described by using different sets coordinate axes having different orientation. Which the following do not depended on the orientation of the axis?
(a) the value of a scalar
(b) component of a vector
(c) a vector
(d) the magnitude of a vector.
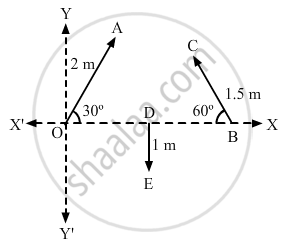
Refer to figure (2 − E1). Find (a) the magnitude, (b) x and y component and (c) the angle with the X-axis of the resultant of \[\overrightarrow{OA}, \overrightarrow{BC} \text { and } \overrightarrow{DE}\].
A mosquito net over a 7 ft × 4 ft bed is 3 ft high. The net has a hole at one corner of the bed through which a mosquito enters the net. It flies and sits at the diagonally opposite upper corner of the net. (a) Find the magnitude of the displacement of the mosquito. (b) Taking the hole as the origin, the length of the bed as the X-axis, it width as the Y axis, and vertically up as the Z-axis, write the components of the displacement vector.
If \[\vec{A} = 2 \vec{i} + 3 \vec{j} + 4 \vec{k} \text { and } \vec{B} = 4 \vec{i} + 3 \vec{j} + 2 \vec{k}\] find \[\vec{A} \times \vec{B}\].
