Advertisements
Advertisements
प्रश्न
Prove that the function f (x) = 5x – 3 is continuous at x = 0, at x = – 3 and at x = 5.
उत्तर
The given function is:
f(x) = 5x - 3
f(0) = 5(0) - 3 = -3
`lim_(x → 0) f(x) = 5(0) - 3 = -3`
`lim_(x → 0) f(x) = f(0)`
Hence, the function is continuous at x = 0
f(-3) = 5(-3) - 3
= -15 - 3
= -18
⇒ `lim_(x → -3) f(x) = 5(-3) - 3`
= -15 - 3
= -18
⇒ `lim_(x → -3) f(x) = f(-3)`
Hence , function is continous at x = -3
f(5) = 5(5) - 3
= 25 - 3
= 22
⇒ `lim_(x → 5) f(x) `
= 5(5) - 3
= 25 - 3
= -22
⇒ `lim_(x → 5) f(x) = f(5)`
Hence , function is continuous at x = 5
APPEARS IN
संबंधित प्रश्न
Find the values of p and q for which
f(x) = `{((1-sin^3x)/(3cos^2x),`
is continuous at x = π/2.
Find all points of discontinuity of f, where f is defined by `f (x) = {(x+1, if x>=1),(x^2+1, if x < 1):}`
Is the function defined by `f(x) = {(x+5, if x <= 1),(x -5, if x > 1):}` a continuous function?
Show that the function defined by g(x) = x = [x] is discontinuous at all integral points. Here [x] denotes the greatest integer less than or equal to x.
Find the points of discontinuity of f, where `f (x) = {(sinx/x, if x<0),(x + 1, if x >= 0):}`
Determine if f defined by `f(x) = {(x^2 sin 1/x, "," if x != 0),(0, "," if x = 0):}` is a continuous function?
For what value of λ is the function
\[f\left( x \right) = \begin{cases}\lambda( x^2 - 2x), & \text{ if } x \leq 0 \\ 4x + 1 , & \text{ if } x > 0\end{cases}\]continuous at x = 0? What about continuity at x = ± 1?
Find the points of discontinuity, if any, of the following functions:
Find the points of discontinuity, if any, of the following functions: \[f\left( x \right) = \begin{cases}2x , & \text{ if } & x < 0 \\ 0 , & \text{ if } & 0 \leq x \leq 1 \\ 4x , & \text{ if } & x > 1\end{cases}\]
Find the points of discontinuity, if any, of the following functions: \[f\left( x \right) = \begin{cases}x^{10} - 1, & \text{ if } x \leq 1 \\ x^2 , & \text{ if } x > 1\end{cases}\]
Find the points of discontinuity, if any, of the following functions: \[f\left( x \right) = \begin{cases}- 2 , & \text{ if }& x \leq - 1 \\ 2x , & \text{ if } & - 1 < x < 1 \\ 2 , & \text{ if } & x \geq 1\end{cases}\]
In the following, determine the value of constant involved in the definition so that the given function is continuou:
The function f (x) = tan x is discontinuous on the set
Discuss the Continuity of the F(X) at the Indicated Points : F(X) = | X − 1 | + | X + 1 | at X = −1, 1.
Show that the function `f(x) = |x-4|, x ∈ R` is continuous, but not diffrent at x = 4.
Show that the function f given by:
`f(x)={((e^(1/x)-1)/(e^(1/x)+1),"if",x,!=,0),(-1,"if",x,=,0):}"`
is discontinuous at x = 0.
Find all points of discontinuity of the function f(t) = `1/("t"^2 + "t" - 2)`, where t = `1/(x - 1)`
`lim_("x" -> pi/2)` [sinx] is equal to ____________.
The number of discontinuous functions y(x) on [-2, 2] satisfying x2 + y2 = 4 is ____________.
Let f (x) `= (1 - "tan x")/(4"x" - pi), "x" ne pi/4, "x" in (0, pi/2).` If f(x) is continuous in `(0, pi/2), "then f"(pi/4) =` ____________.
The function `f(x) = (x^2 - 25)/(x + 5)` is continuous at x =
The function f defined by `f(x) = {{:(x, "if" x ≤ 1),(5, "if" x > 1):}` discontinuous at x equal to
The point of discountinuity of the function `f(x) = {{:(2x + 3",", x ≤ 2),(2x - 3",", x > 2):}` is are
How many point of discontinuity for the following function for x ∈ R
`f(x) = {{:(x + 1",", if x ≥ 1),(x^2 + 1",", if x < 1):}`
`f(x) = {{:(x^10 - 1",", if x ≤ 1),(x^2",", if x > 1):}` is discontinuous at
Let a, b ∈ R, b ≠ 0. Define a function
F(x) = `{{:(asin π/2(x - 1)",", "for" x ≤ 0),((tan2x - sin2x)/(bx^3)",", "for" x > 0):}`
If f is continuous at x = 0, then 10 – ab is equal to ______.
If functions g and h are defined as
g(x) = `{{:(x^2 + 1, x∈Q),(px^2, x\cancel(∈)Q):}`
and h(x) = `{{:(px, x∈Q),(2x + q, x\cancel(∈)Q):}`
If (g + h)(x) is continuous at x = 1 and x = 3, then 3p + q is ______.
If f(x) = `{{:(cos ((π(sqrt(1 + x) - 1))/x)/x,",", x ≠ 0),(π/k,",", x = 0):}`
is continuous at x = 0, then k2 is equal to ______.
Find the value of k for which the function f given as
f(x) =`{{:((1 - cosx)/(2x^2)",", if x ≠ 0),( k",", if x = 0 ):}`
is continuous at x = 0.
If f(x) = `{{:((kx)/|x|"," if x < 0),( 3"," if x ≥ 0):}` is continuous at x = 0, then the value of k is ______.
The graph of the function f is shown below.
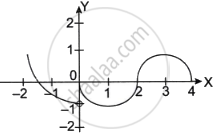
Of the following options, at what values of x is the function f NOT differentiable?
