Advertisements
Advertisements
प्रश्न
Prove that the function f (x) = 5x – 3 is continuous at x = 0, at x = – 3 and at x = 5.
उत्तर
The given function is:
f(x) = 5x - 3
f(0) = 5(0) - 3 = -3
`lim_(x → 0) f(x) = 5(0) - 3 = -3`
`lim_(x → 0) f(x) = f(0)`
Hence, the function is continuous at x = 0
f(-3) = 5(-3) - 3
= -15 - 3
= -18
⇒ `lim_(x → -3) f(x) = 5(-3) - 3`
= -15 - 3
= -18
⇒ `lim_(x → -3) f(x) = f(-3)`
Hence , function is continous at x = -3
f(5) = 5(5) - 3
= 25 - 3
= 22
⇒ `lim_(x → 5) f(x) `
= 5(5) - 3
= 25 - 3
= -22
⇒ `lim_(x → 5) f(x) = f(5)`
Hence , function is continuous at x = 5
APPEARS IN
संबंधित प्रश्न
Discuss the continuity of the following functions. If the function have a removable discontinuity, redefine the function so as to remove the discontinuity
`f(x)=(4^x-e^x)/(6^x-1)` for x ≠ 0
`=log(2/3) ` for x=0
Is the function f defined by f(x)= `{(x, if x<=1),(5, if x > 1):}` continuous at x = 0? At x = 1? At x = 2?
Find all point of discontinuity of f, where f is defined by `f (x) = {(2x + 3, if x<=2),(2x - 3, if x > 2):}`
Find all points of discontinuity of f, where f is defined by `f (x) = {(x^10 - 1, if x<=1),(x^2, if x > 1):}`
Is the function defined by `f(x) = {(x+5, if x <= 1),(x -5, if x > 1):}` a continuous function?
Determine if f defined by `f(x) = {(x^2 sin 1/x, "," if x != 0),(0, "," if x = 0):}` is a continuous function?
Examine the continuity of f, where f is defined by `f(x) = {(sin x - cos x, if x != 0),(-1, "," if x = 0):}`
Find all the points of discontinuity of f defined by `f(x) = |x| - |x + 1|`.
Determine the value of the constant 'k' so that function f(x) `{((kx)/|x|, ","if x < 0),(3"," , if x >= 0):}` is continuous at x = 0
Find the value of constant ‘k’ so that the function f (x) defined as
f(x) = `{((x^2 -2x-3)/(x+1), x != -1),(k, x != -1):}`
is continous at x = -1
Test the continuity of the function on f(x) at the origin:
\[f\left( x \right) = \begin{cases}\frac{x}{\left| x \right|}, & x \neq 0 \\ 1 , & x = 0\end{cases}\]
Prove that the function
Find the relationship between 'a' and 'b' so that the function 'f' defined by
In the following, determine the value of constant involved in the definition so that the given function is continuou:
Discuss the Continuity of the F(X) at the Indicated Points : F(X) = | X − 1 | + | X + 1 | at X = −1, 1.
Find the point of discontinuity, if any, of the following function: \[f\left( x \right) = \begin{cases}\sin x - \cos x , & \text{ if } x \neq 0 \\ - 1 , & \text{ if } x = 0\end{cases}\]
Show that the function `f(x) = |x-4|, x ∈ R` is continuous, but not diffrent at x = 4.
Prove that `1/2 "cos"^(-1) ((1-"x")/(1+"x")) = "tan"^-1 sqrt"x"`
Show that the function f given by:
`f(x)={((e^(1/x)-1)/(e^(1/x)+1),"if",x,!=,0),(-1,"if",x,=,0):}"`
is discontinuous at x = 0.
Find all points of discontinuity of the function f(t) = `1/("t"^2 + "t" - 2)`, where t = `1/(x - 1)`
Let f (x) `= (1 - "tan x")/(4"x" - pi), "x" ne pi/4, "x" in (0, pi/2).` If f(x) is continuous in `(0, pi/2), "then f"(pi/4) =` ____________.
If f(x) `= sqrt(4 + "x" - 2)/"x", "x" ne 0` be continuous at x = 0, then f(0) = ____________.
`lim_("x"-> 0) sqrt(1/2 (1 - "cos" 2"x"))/"x"` is equal to
`f(x) = {{:(x^3 - 3",", if x < 2),(x^2 + 1",", if x > 2):}` has how many point of discontinuity
Let a, b ∈ R, b ≠ 0. Define a function
F(x) = `{{:(asin π/2(x - 1)",", "for" x ≤ 0),((tan2x - sin2x)/(bx^3)",", "for" x > 0):}`
If f is continuous at x = 0, then 10 – ab is equal to ______.
If function f(x) = `{{:((asinx + btanx - 3x)/x^3,",", x ≠ 0),(0,",", x = 0):}` is continuous at x = 0 then (a2 + b2) is equal to ______.
If f(x) = `{{:(cos ((π(sqrt(1 + x) - 1))/x)/x,",", x ≠ 0),(π/k,",", x = 0):}`
is continuous at x = 0, then k2 is equal to ______.
If f(x) = `{{:((log_(sin|x|) cos^2x)/(log_(sin|3x|) cos x/2), |x| < π/3; x ≠ 0),(k, x = 0):}`, then value of k for which f(x) is continuous at x = 0 is ______.
If the function f defined as f(x) = `1/x - (k - 1)/(e^(2x) - 1)` x ≠ 0, is continuous at x = 0, then the ordered pair (k, f(0)) is equal to ______.
Find the value of k for which the function f given as
f(x) =`{{:((1 - cosx)/(2x^2)",", if x ≠ 0),( k",", if x = 0 ):}`
is continuous at x = 0.
If f(x) = `{{:((kx)/|x|"," if x < 0),( 3"," if x ≥ 0):}` is continuous at x = 0, then the value of k is ______.
The graph of the function f is shown below.
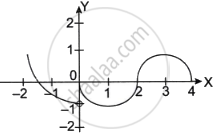
Of the following options, at what values of x is the function f NOT differentiable?
