Advertisements
Advertisements
प्रश्न
Is the function f defined by f(x)= `{(x, if x<=1),(5, if x > 1):}` continuous at x = 0? At x = 1? At x = 2?
उत्तर
`f (x) = {(x, if x<=1),(5, if x > 1):}`
(i) ⇒ x = 0 पर
`lim_(x -> 0^-) f (x) = lim_(h -> 0) f(0 - h)`
= 0 - 0
= 0
`lim_(x -> 0^+) f(x) = lim_(h -> 0) f(0 + h)`
= 0 + 0
= 0
f(0) = 0
(ii) Hence, f is continuous at x = 0.
⇒ at x = 1
`lim_(x -> 1)` f(x) = `lim_(h -> 1)` f (1 - h)
= 1 - 0
= 1
`lim_(x -> 1)` f(x) = 5
Hence f is not continuous at x = 1.
⇒ at x = 2
`lim_(x -> 2^-)` f(x) = `lim_(h -> 2^+)` f(x) = 5
f(2) = 5
Hence, f is continuous at x = 2.
APPEARS IN
संबंधित प्रश्न
Discuss the continuity of the following functions. If the function have a removable discontinuity, redefine the function so as to remove the discontinuity
`f(x)=(4^x-e^x)/(6^x-1)` for x ≠ 0
`=log(2/3) ` for x=0
Find the values of p and q for which
f(x) = `{((1-sin^3x)/(3cos^2x),`
is continuous at x = π/2.
Prove that the function f (x) = 5x – 3 is continuous at x = 0, at x = – 3 and at x = 5.
Examine the continuity of the function f(x) = 2x2 – 1 at x = 3.
Find all point of discontinuity of f, where f is defined by `f (x) = {(2x + 3, if x<=2),(2x - 3, if x > 2):}`
Find all points of discontinuity of f, where f is defined by `f (x) = {(x^10 - 1, if x<=1),(x^2, if x > 1):}`
Show that the function defined by g(x) = x = [x] is discontinuous at all integral points. Here [x] denotes the greatest integer less than or equal to x.
Examine the continuity of f, where f is defined by `f(x) = {(sin x - cos x, if x != 0),(-1, "," if x = 0):}`
Find all the points of discontinuity of f defined by `f(x) = |x| - |x + 1|`.
Determine the value of the constant 'k' so that function f(x) `{((kx)/|x|, ","if x < 0),(3"," , if x >= 0):}` is continuous at x = 0
Find the value of constant ‘k’ so that the function f (x) defined as
f(x) = `{((x^2 -2x-3)/(x+1), x != -1),(k, x != -1):}`
is continous at x = -1
Show that the function f(x) = `{(x^2, x<=1),(1/2, x>1):}` is continuous at x = 1 but not differentiable.
Prove that the function
Find the relationship between 'a' and 'b' so that the function 'f' defined by
Find the points of discontinuity, if any, of the following functions: \[f\left( x \right) = \begin{cases}2x , & \text{ if } & x < 0 \\ 0 , & \text{ if } & 0 \leq x \leq 1 \\ 4x , & \text{ if } & x > 1\end{cases}\]
Find the points of discontinuity, if any, of the following functions: \[f\left( x \right) = \begin{cases}- 2 , & \text{ if }& x \leq - 1 \\ 2x , & \text{ if } & - 1 < x < 1 \\ 2 , & \text{ if } & x \geq 1\end{cases}\]
The function f (x) = tan x is discontinuous on the set
Discuss the Continuity of the F(X) at the Indicated Points : F(X) = | X − 1 | + | X + 1 | at X = −1, 1.
If f(x) = `{{:("a"x + 1, "if" x ≥ 1),(x + 2, "if" x < 1):}` is continuous, then a should be equal to ______.
Let f (x) `= (1 - "tan x")/(4"x" - pi), "x" ne pi/4, "x" in (0, pi/2).` If f(x) is continuous in `(0, pi/2), "then f"(pi/4) =` ____________.
`lim_("x"-> 0) sqrt(1/2 (1 - "cos" 2"x"))/"x"` is equal to
The function f defined by `f(x) = {{:(x, "if" x ≤ 1),(5, "if" x > 1):}` discontinuous at x equal to
The point of discountinuity of the function `f(x) = {{:(2x + 3",", x ≤ 2),(2x - 3",", x > 2):}` is are
How many point of discontinuity for the following function in its. domain.
`f(x) = {{:(x/|x|",", if x < 0),(-1",", if x ≥ 0):}`
How many point of discontinuity for the following function for x ∈ R
`f(x) = {{:(x + 1",", if x ≥ 1),(x^2 + 1",", if x < 1):}`
`f(x) = {{:(x^3 - 3",", if x < 2),(x^2 + 1",", if x > 2):}` has how many point of discontinuity
`f(x) = {{:(x^10 - 1",", if x ≤ 1),(x^2",", if x > 1):}` is discontinuous at
If functions g and h are defined as
g(x) = `{{:(x^2 + 1, x∈Q),(px^2, x\cancel(∈)Q):}`
and h(x) = `{{:(px, x∈Q),(2x + q, x\cancel(∈)Q):}`
If (g + h)(x) is continuous at x = 1 and x = 3, then 3p + q is ______.
If the function f defined as f(x) = `1/x - (k - 1)/(e^(2x) - 1)` x ≠ 0, is continuous at x = 0, then the ordered pair (k, f(0)) is equal to ______.
Find the value(s) of 'λ' if the function
f(x) = `{{:((sin^2 λx)/x^2",", if x ≠ 0 "is continuous at" x = 0.),(1",", if x = 0):}`
Find the value of k for which the function f given as
f(x) =`{{:((1 - cosx)/(2x^2)",", if x ≠ 0),( k",", if x = 0 ):}`
is continuous at x = 0.
The graph of the function f is shown below.
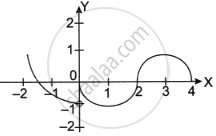
Of the following options, at what values of x is the function f NOT differentiable?
Consider the graph `y = x^(1/3)`
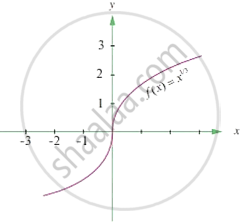
Statement 1: The above graph is continuous at x = 0
Statement 2: The above graph is differentiable at x = 0
Which of the following is correct?
