Advertisements
Advertisements
प्रश्न
Find the points of discontinuity, if any, of the following functions:
उत्तर
The given function f is
The given function is defined at all points of the real line.
Let c be a point on the real line.
Case I:
Therefore, f is continuous at all points x, such that x < −1
Case II:
The left hand limit of f at x = −1 is,
The right hand limit of f at x = −1 is,
Therefore, f is continuous at x = −1
Case III:
Therefore, f is continuous at all points of the interval (−1, 1).
Case IV:
The left hand limit of f at x = 1 is,
The right hand limit of f at x = 1 is,
Therefore, f is continuous at x = 2
Case V:
Therefore, f is continuous at all points x, such that x > 1
Thus, from the above observations, it can be concluded that f is continuous at all points of the real line.
APPEARS IN
संबंधित प्रश्न
Examine the continuity of the function f(x) = 2x2 – 1 at x = 3.
Prove that the function
Find all point of discontinuity of f, where f is defined by
Find all points of discontinuity of f, where f is defined by
Find all points of discontinuity of f, where f is defined by
Find all points of discontinuity of f, where f is defined by
Find all points of discontinuity of f, where f is defined by
Find the points of discontinuity of f, where
Find all the points of discontinuity of f defined by
Using mathematical induction prove that
Find the value of constant ‘k’ so that the function f (x) defined as
f(x) =
is continous at x = -1
Show that the function f(x) =
Test the continuity of the function on f(x) at the origin:
For what value of λ is the function
Find the relationship between 'a' and 'b' so that the function 'f' defined by
Find the points of discontinuity, if any, of the following functions:
In the following, determine the value of constant involved in the definition so that the given function is continuou:
Discuss the Continuity of the F(X) at the Indicated Points : F(X) = | X − 1 | + | X + 1 | at X = −1, 1.
If f(x) =
The number of discontinuous functions y(x) on [-2, 2] satisfying x2 + y2 = 4 is ____________.
Let f (x)
If f(x)
The domain of the function f(x) =
How many point of discontinuity for the following function in its. domain.
Let a, b ∈ R, b ≠ 0. Define a function
F(x) =
If f is continuous at x = 0, then 10 – ab is equal to ______.
If function f(x) =
Let α ∈ R be such that the function
f(x) =
is continuous at x = 0, where {x} = x – [x], [x] is the greatest integer less than or equal to x.
Find the value of k for which the function f given as
f(x) =
is continuous at x = 0.
The graph of the function f is shown below.
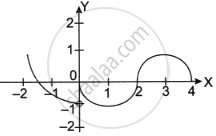
Of the following options, at what values of x is the function f NOT differentiable?
