Advertisements
Advertisements
प्रश्न
Determine if f defined by `f(x) = {(x^2 sin 1/x, "," if x != 0),(0, "," if x = 0):}` is a continuous function?
उत्तर
We have f (0) = 0
`lim_(x->0^-) f (x) = lim_(h->0)(0 - h^2) sin 1/-h = h^2 sin (1/h)`
but `sin 1/h ∈ [-1, 1]`
= `h^2 sin 1/h -> 0` as h ->0.
`lim_(x->0^+) f (x) = lim_(h->0) (0 + h)^2 sin 1/h =h^2 sin 1/h = 0 `
= `lim_(x->0^-) f (x) = lim_(x->0^+) f (x) = f (0)`
= f is continuous at x = 0
APPEARS IN
संबंधित प्रश्न
Discuss the continuity of the following functions. If the function have a removable discontinuity, redefine the function so as to remove the discontinuity
`f(x)=(4^x-e^x)/(6^x-1)` for x ≠ 0
`=log(2/3) ` for x=0
Show that the function `f(x)=|x-3|,x in R` is continuous but not differentiable at x = 3.
Is the function f defined by f(x)= `{(x, if x<=1),(5, if x > 1):}` continuous at x = 0? At x = 1? At x = 2?
Find all point of discontinuity of f, where f is defined by `f (x) = {(2x + 3, if x<=2),(2x - 3, if x > 2):}`
Find all points of discontinuity of f, where f is defined by `f(x) = {(|x|+3, if x<= -3),(-2x, if -3 < x < 3),(6x + 2, if x >= 3):}`
Find all points of discontinuity of f, where f is defined by `f(x) = {(|x|/x , if x != 0),(0, if x = 0):}`
Find all points of discontinuity of f, where f is defined by `f (x) = {(x+1, if x>=1),(x^2+1, if x < 1):}`
Is the function defined by `f(x) = {(x+5, if x <= 1),(x -5, if x > 1):}` a continuous function?
Find the points of discontinuity of f, where `f (x) = {(sinx/x, if x<0),(x + 1, if x >= 0):}`
Test the continuity of the function on f(x) at the origin:
\[f\left( x \right) = \begin{cases}\frac{x}{\left| x \right|}, & x \neq 0 \\ 1 , & x = 0\end{cases}\]
Prove that the function
Find the relationship between 'a' and 'b' so that the function 'f' defined by
In the following, determine the value of constant involved in the definition so that the given function is continuou:
The function f (x) = tan x is discontinuous on the set
Discuss the Continuity of the F(X) at the Indicated Points : F(X) = | X − 1 | + | X + 1 | at X = −1, 1.
Find the point of discontinuity, if any, of the following function: \[f\left( x \right) = \begin{cases}\sin x - \cos x , & \text{ if } x \neq 0 \\ - 1 , & \text{ if } x = 0\end{cases}\]
Show that the function `f(x) = |x-4|, x ∈ R` is continuous, but not diffrent at x = 4.
Show that the function f given by:
`f(x)={((e^(1/x)-1)/(e^(1/x)+1),"if",x,!=,0),(-1,"if",x,=,0):}"`
is discontinuous at x = 0.
If f(x) = `{{:("a"x + 1, "if" x ≥ 1),(x + 2, "if" x < 1):}` is continuous, then a should be equal to ______.
Find all points of discontinuity of the function f(t) = `1/("t"^2 + "t" - 2)`, where t = `1/(x - 1)`
`lim_("x" -> pi/2)` [sinx] is equal to ____________.
The domain of the function f(x) = `""^(24 - x)C_(3x - 1) + ""^(40 - 6x)C_(8x - 10)` is
The function f defined by `f(x) = {{:(x, "if" x ≤ 1),(5, "if" x > 1):}` discontinuous at x equal to
The point of discountinuity of the function `f(x) = {{:(2x + 3",", x ≤ 2),(2x - 3",", x > 2):}` is are
`f(x) = {{:(x^10 - 1",", if x ≤ 1),(x^2",", if x > 1):}` is discontinuous at
Let a, b ∈ R, b ≠ 0. Define a function
F(x) = `{{:(asin π/2(x - 1)",", "for" x ≤ 0),((tan2x - sin2x)/(bx^3)",", "for" x > 0):}`
If f is continuous at x = 0, then 10 – ab is equal to ______.
If function f(x) = `{{:((asinx + btanx - 3x)/x^3,",", x ≠ 0),(0,",", x = 0):}` is continuous at x = 0 then (a2 + b2) is equal to ______.
If f(x) = `{{:(cos ((π(sqrt(1 + x) - 1))/x)/x,",", x ≠ 0),(π/k,",", x = 0):}`
is continuous at x = 0, then k2 is equal to ______.
If f(x) = `{{:((log_(sin|x|) cos^2x)/(log_(sin|3x|) cos x/2), |x| < π/3; x ≠ 0),(k, x = 0):}`, then value of k for which f(x) is continuous at x = 0 is ______.
If the function f defined as f(x) = `1/x - (k - 1)/(e^(2x) - 1)` x ≠ 0, is continuous at x = 0, then the ordered pair (k, f(0)) is equal to ______.
Find the value(s) of 'λ' if the function
f(x) = `{{:((sin^2 λx)/x^2",", if x ≠ 0 "is continuous at" x = 0.),(1",", if x = 0):}`
The graph of the function f is shown below.
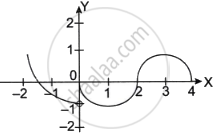
Of the following options, at what values of x is the function f NOT differentiable?
Consider the graph `y = x^(1/3)`
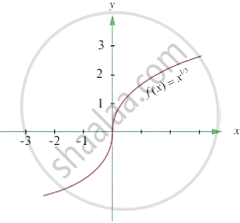
Statement 1: The above graph is continuous at x = 0
Statement 2: The above graph is differentiable at x = 0
Which of the following is correct?
