Advertisements
Advertisements
प्रश्न
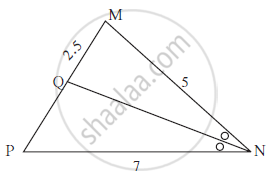
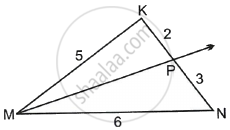
Seg NQ is the bisector of ∠ N
of Δ MNP. If MN= 5, PN =7,
MQ = 2.5 then find QP.
उत्तर
MN = 5, PN = 7, MQ = 2.5, QP = ?
From the figure `(MN)/(NP)=(MQ)/(QP)`= ..............(Angle bisector theorem)
∴ `5/2.5 = 7/(QP)`
∴ 5 × QP = 7 × 2.5
∴ QP = `(7×2.5)/5`.
∴ QP = 3.5
APPEARS IN
संबंधित प्रश्न
Given below is the triangle and length of line segments. Identify in the given figure, ray PM is the bisector of ∠QPR.

Given below is the triangle and length of line segments. Identify in the given figure, ray PM is the bisector of ∠QPR.

Given below is the triangle and length of line segments. Identify in the given figure, ray PM is the bisector of ∠QPR.

In ∆MNP, NQ is a bisector of ∠N. If MN = 5, PN = 7 MQ = 2.5 then find QP.
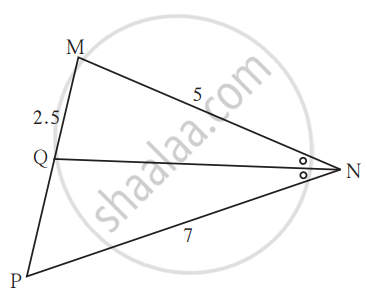
Find QP using given information in the figure.

In the given figure, if AB || CD || FE then find x and AE.

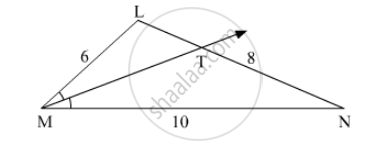
In ∆LMN, ray MT bisects ∠LMN If LM = 6, MN = 10, TN = 8, then Find LT.
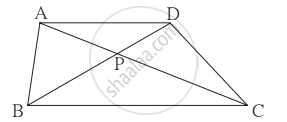
In ▢ABCD, seg AD || seg BC. Diagonal AC and diagonal BD intersect each other in point P. Then show that `"AP"/"PD" = "PC"/"BP"`.
From the top of a light house, an abserver looking at a boat makes an angle of depression of 600. If the height of the lighthouse is 90 m then find how far is the boat from the lighthouse. (3 = 1.73)

In ΔABC, ray BD bisects ∠ABC.
If A – D – C, A – E – B and seg ED || side BC, then prove that:
`("AB")/("BC") = ("AE")/("EB")`
Proof :
In ΔABC, ray BD bisects ∠ABC.
∴ `("AB")/("BC") = (......)/(......)` ......(i) (By angle bisector theorem)
In ΔABC, seg DE || side BC
∴ `("AE")/("EB") = ("AD")/("DC")` ....(ii) `square`
∴ `("AB")/square = square/("EB")` [from (i) and (ii)]
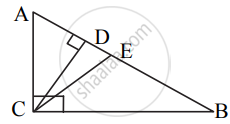
In ΔABC, ∠ACB = 90°. seg CD ⊥ side AB and seg CE is angle bisector of ∠ACB.
Prove that: `(AD)/(BD) = (AE^2)/(BE^2)`.
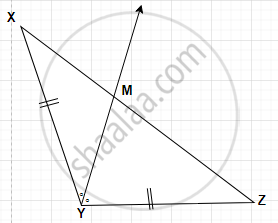
In the figure, ray YM is the bisector of ∠XYZ, where seg XY ≅ seg YZ, find the relation between XM and MZ.
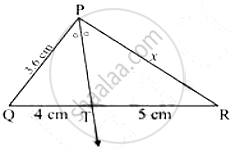
In the following figure, ray PT is the bisector of ∠QPR Find the value of x and perimeter of ∠QPR.
From the information given in the figure, determine whether MP is the bisector of ∠KMN.
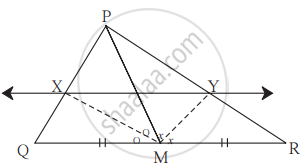
In ∆PQR seg PM is a median. Angle bisectors of ∠PMQ and ∠PMR intersect side PQ and side PR in points X and Y respectively. Prove that XY || QR.
Complete the proof by filling in the boxes.
solution:
In ∆PMQ,
Ray MX is the bisector of ∠PMQ.
∴ `("MP")/("MQ") = square/square` .............(I) [Theorem of angle bisector]
Similarly, in ∆PMR, Ray MY is the bisector of ∠PMR.
∴ `("MP")/("MR") = square/square` .............(II) [Theorem of angle bisector]
But `("MP")/("MQ") = ("MP")/("MR")` .............(III) [As M is the midpoint of QR.]
Hence MQ = MR
∴ `("PX")/square = square/("YR")` .............[From (I), (II) and (III)]
∴ XY || QR .............[Converse of basic proportionality theorem]

In ΔABC, ray BD bisects ∠ABC, A – D – C, seg DE || side BC, A – E – B, then for showing `("AB")/("BC") = ("AE")/("EB")`, complete the following activity:
Proof :
In ΔABC, ray BD bisects ∠B.
∴ `square/("BC") = ("AD")/("DC")` ...(I) (`square`)
ΔABC, DE || BC
∴ `(square)/("EB") = ("AD")/("DC")` ...(II) (`square`)
∴ `("AB")/square = square/("EB")` ...[from (I) and (II)]
