Advertisements
Advertisements
प्रश्न
Show that `sin^-1 (- 3/5) - sin^-1 (- 8/17) = cos^-1 (84/85)`
उत्तर
`sin^-1 (- 3/5) - sin^-1 (- 8/17)`
= `- sin^-1 (3/5) + sin^-1 (8/17)`
= `sin^-1 (8/17) - sin^-1 (3/5)`
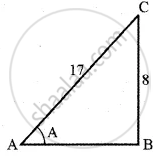
AB = `sqrt(17^2 - 8^2) = sqrt225` = 15
Let `sin^-1 (8/17)` = A
`8/17` = sin A
sin A = `8/17`
∴ cos A = `15/17`
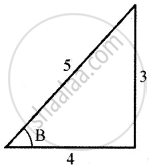
Let `sin^-1 (3/5)` = B
sin B = `3/5`
∴ cos B = `4/5`
Consider cos(A – B) = cos A cos B + sin A sin B
`= 15/17 xx 4/5 + 8/17 xx 3/5`
`= 60/85 + 24/85`
cos (A – B) = `84/85`
∴ A – B = `cos^-1 (84/85)`
i.e., `sin^-1 (8/17) - sin^-1 (3/5) = cos^-1 (84/85)`
i.e., `sin^-1 (-3/5) - sin^-1 (-8/17) = cos^-1 (84/85)`
APPEARS IN
संबंधित प्रश्न
Find the principal value of `cos^(-1) (-1/sqrt2)`
Evaluate the following:
`cot^-1{2cos(sin^-1 sqrt3/2)}`
Find the principal value of the following: tan-1(– 1)
Prove the following:
`cos^-1(3/5) + cos^-1(4/5) = pi/(2)`
Find the principal value of `cos^-1 sqrt(3)/2`
In Δ ABC, with the usual notations, if sin B sin C = `"bc"/"a"^2`, then the triangle is ______.
The value of `cos(pi/4 + x) - cos(pi/4 - x)` is ______.
If `"sin"^-1("x"^2 - 7"x" + 12) = "n"pi, AA "n" in "I"`, then x = ____________.
Value of `sin(pi/3 - sin^1 (- 1/2))` is equal to
The value of `cos^-1(cos(π/2)) + cos^-1(sin((2π)/2))` is ______.
