Advertisements
Advertisements
Question
Show that `sin^-1 (- 3/5) - sin^-1 (- 8/17) = cos^-1 (84/85)`
Solution
`sin^-1 (- 3/5) - sin^-1 (- 8/17)`
= `- sin^-1 (3/5) + sin^-1 (8/17)`
= `sin^-1 (8/17) - sin^-1 (3/5)`
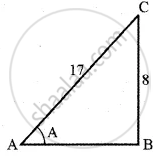
AB = `sqrt(17^2 - 8^2) = sqrt225` = 15
Let `sin^-1 (8/17)` = A
`8/17` = sin A
sin A = `8/17`
∴ cos A = `15/17`
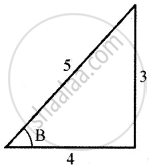
Let `sin^-1 (3/5)` = B
sin B = `3/5`
∴ cos B = `4/5`
Consider cos(A – B) = cos A cos B + sin A sin B
`= 15/17 xx 4/5 + 8/17 xx 3/5`
`= 60/85 + 24/85`
cos (A – B) = `84/85`
∴ A – B = `cos^-1 (84/85)`
i.e., `sin^-1 (8/17) - sin^-1 (3/5) = cos^-1 (84/85)`
i.e., `sin^-1 (-3/5) - sin^-1 (-8/17) = cos^-1 (84/85)`
APPEARS IN
RELATED QUESTIONS
Evaluate the following:
`tan^-1(-1/sqrt3)+cot^-1(1/sqrt3)+tan^-1(sin(-pi/2))`
Find the principal solutions of the following equation:
sin 2θ = `− 1/(sqrt2)`
Evaluate:
`sin[cos^-1 (3/5)]`
Prove that `2 tan^-1 (1/8) + tan^-1 (1/7) + 2tan^-1 (1/5) = pi/4`
In Δ ABC, with the usual notations, if sin B sin C = `"bc"/"a"^2`, then the triangle is ______.
The value of cot (- 1110°) is equal to ______.
Solve for x `tan^-1((1 - x)/(1 + x)) = 1/2 tan^-1x, x > 0`
The domain of y = cos–1(x2 – 4) is ______.
`"sin"^-1 (-1/2)`
If tan-1 (x – 1) + tan-1 x + tan-1 (x + 1) = tan-1 3x, then the values of x are ____________.
