Advertisements
Advertisements
प्रश्न
Show that `sin^-1 (- 3/5) - sin^-1 (- 8/17) = cos^-1 (84/85)`
उत्तर
`sin^-1 (- 3/5) - sin^-1 (- 8/17)`
= `- sin^-1 (3/5) + sin^-1 (8/17)`
= `sin^-1 (8/17) - sin^-1 (3/5)`
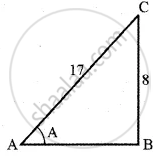
AB = `sqrt(17^2 - 8^2) = sqrt225` = 15
Let `sin^-1 (8/17)` = A
`8/17` = sin A
sin A = `8/17`
∴ cos A = `15/17`
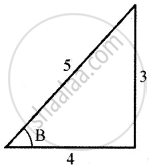
Let `sin^-1 (3/5)` = B
sin B = `3/5`
∴ cos B = `4/5`
Consider cos(A – B) = cos A cos B + sin A sin B
`= 15/17 xx 4/5 + 8/17 xx 3/5`
`= 60/85 + 24/85`
cos (A – B) = `84/85`
∴ A – B = `cos^-1 (84/85)`
i.e., `sin^-1 (8/17) - sin^-1 (3/5) = cos^-1 (84/85)`
i.e., `sin^-1 (-3/5) - sin^-1 (-8/17) = cos^-1 (84/85)`
APPEARS IN
संबंधित प्रश्न
Find the value of the following:
`tan^(-1)(1) + cos^(-1) (-1/2) + sin^(-1) (-1/2)`
Find the principal value of `sin^-1(1/sqrt2)`
Find the principal value of the following: cosec- 1(2)
Evaluate cot(tan−1(2x) + cot−1(2x))
Prove that `2 tan^-1 (3/4) = tan^-1(24/7)`
The principle solutions of equation tan θ = -1 are ______
Prove that `cot(pi/4 - 2cot^-1 3)` = 7
Find the principal value of `cot^-1 ((-1)/sqrt(3))`
If sin–1x – cos–1x = `π/6`, then x = ______.
Find the value of `tan^-1(x/y) + tan^-1((y - x)/(y + x))`
