Advertisements
Advertisements
प्रश्न
State Kepler's law of orbit and law of equal areas.
उत्तर १
Ist law ( Law of orbit ) : The orbital path in the solar system is an ellipse with sun as one focus.
2nd law ( Law of equal area ) : The radius vector joining the centre of the planet to the centre of sun traces out equal area in equal intervals of time.
i.e.The area velocity of the planet is constant
उत्तर २
All planet revolves around the sun in the elliptical orbit, the sun as one of its focus.
The line joining sun and planet sweeps the equal area in equal time interval i.e. Areal velocity is constant.
APPEARS IN
संबंधित प्रश्न
Let us assume that our galaxy consists of 2.5 × 1011 stars each of one solar mass. How long will a star at a distance of 50,000 ly from the galactic centre take to complete one revolution? Take the diameter of the Milky Way to be 105 ly
A comet orbits the Sun in a highly elliptical orbit. Does the comet have a constant (a) linear speed, (b) angular speed, (c) angular momentum, (d) kinetic energy, (e) potential energy, (f) total energy throughout its orbit? Neglect any mass loss of the comet when it comes very close to the Sun.
State Kepler's laws of planetary motion.
Identify the law shown in the figure and state three respective laws.
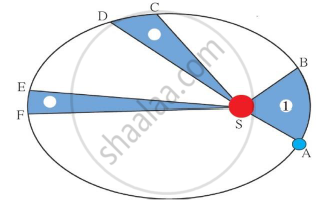
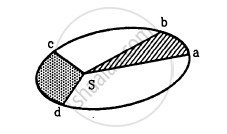
In the Following figure shows the elliptical path of a planet about the sun. The two shaded parts have equal area. If t1 and t2 be the time taken by the planet to go from a to b and from c to d respectively,
Answer the following question.
State Kepler’s law of the period.
Write the Kepler's laws.
The third law of Kepler is also known as the Law of ______.
State Kepler’s laws.
If the distance between the sun and the earth is made three times, then attraction between the two will ______
A planet is revolving around the sun in an elliptical orbit as shown in figure. At which point will its K.E. be maximum?
The mass and radius of earth is 'Me' and 'Re' respectively and that of moon is 'Mm' and 'Rm' respectively. The distance between the centre of the earth and that of moon is 'D'. The minimum speed required for a body (mass 'm') to project from a point midway between their centres to escape to infinity is ______.
A planet revolves in an elliptical orbit around the sun. The semi-major and minor axes are a and b, then the time period is given by:
In our solar system, the inter-planetary region has chunks of matter (much smaller in size compared to planets) called asteroids. They ______.
If the sun and the planets carried huge amounts of opposite charges ______.
- all three of Kepler’s laws would still be valid.
- only the third law will be valid.
- the second law will not change.
- the first law will still be valid.
Supposing Newton’s law of gravitation for gravitation forces F1 and F2 between two masses m1 and m2 at positions r1 and r2 read F1 = – F2 = `- r_12/r_12^3 GM_0^2 ((m_1m_2)/M_0^2)^n` where M0 is a constant of dimension of mass r12 = r1 – r2 and n is a number. in such a case.
- the acceleration due to gravity on earth will be different for different objects.
- none of the three laws of Kepler will be valid.
- only the third law will become invalid.
- for n negative, an object lighter than water will sink in water.
The centre of mass of an extended body on the surface of the earth and its centre of gravity ______.
- are always at the same point for any size of the body.
- are always at the same point only for spherical bodies.
- can never be at the same point.
- is close to each other for objects, say of sizes less than 100 m.
- both can change if the object is taken deep inside the earth.
Give one example each of central force and non-central force.
Draw areal velocity versus time graph for mars.
A satellite is in an elliptic orbit around the earth with aphelion of 6R and perihelion of 2 R where R= 6400 km is the radius of the earth. Find eccentricity of the orbit. Find the velocity of the satellite at apogee and perigee. What should be done if this satellite has to be transferred to a circular orbit of radius 6R ?
[G = 6.67 × 10–11 SI units and M = 6 × 1024 kg]
The maximum and minimum distances of a comet from the Sun are 1.6 × 1012 m and 8.0 × 1010 m respectively. If the speed of the comet at the nearest point is 6 × 104 ms-1, the speed at the farthest point is ______.
Two planets A and B of equal mass are having their period of revolutions TA and TB such that TA = 2TB. These planets are revolving in the circular orbits of radii rA and rB respectively. Which out of the following would be the correct relationship of their orbits?
