Advertisements
Advertisements
प्रश्न
The circumference of the base of a 12 m high conical tent is 66 m. Find the volume of the air contained in it.
उत्तर
Given, Circumference of conical tent C = 66 m
And height (h) of conical tent = 12 m.
∴ Radius = `C/(2pi)`
= `(66 xx 7)/(2 xx 22)`
= `21/2`
= 10.5 m
∴ Volume of the air contained by it
= `1/3 pir^2h`
= `1/3 xx 22/7 xx 21/2 xx 21/2 xx 12 m^3`
= 1386 m3
APPEARS IN
संबंधित प्रश्न
A conical tent is 10 m high and the radius of its base is 24 m. Find
- slant height of the tent.
- cost of the canvas required to make the tent, if the cost of 1 m2 canvas is ₹ 70.
`["Assume "pi=22/7]`
Find the curved surface area of a cone with base radius 5.25 cm and slant height 10cm.
A cylinder and a cone have equal radii of their bases and equal heights. If their curved surface areas are in the ratio 8:5, show that the radius of each is to the height of each as 3:4.
The ratio of volumes of two cones is 4 : 5 and the ratio of the radii of their bases is 2:3. Find the ratio of their vertical heights.
The volume of a right circular cone is 9856 cm3. If the diameter of the base is 28 cm, find:
(i) height of the cone (ii) slant height of the cone (iii) curved surface area of the cone.
A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilo litres?
The diameter of two cones are equal. If their slant heights are in the ratio 5 : 4, find the ratio of their curved surface areas.
There are two cones. The curved surface area of one is twice that of the other. The slant height of the latter is twice that of the former. Find the ratio of their radii.
Find what length of canvas, 1.5 m in width, is required to make a conical tent 48 m in diameter and 7 m in height. Given that 10% of the canvas is used in folds and stitchings. Also, find the cost of the canvas at the rate of Rs. 24 per metre.
A solid cone of height 8 cm and base radius 6 cm is melted and recast into identical cones, each of height 2 cm and diameter 1 cm. Find the number of cones formed.
The volume of a conical tent is 1232 m3 and the area of the base floor is 154 m2. Calculate the:
- radius of the floor,
- height of the tent,
- length of the canvas required to cover this conical tent if its width is 2 m.
A solid metallic hemisphere of diameter 28 cm is melted and recast into a number of identical solid cones, each of diameter 14 cm and height 8 cm. Find the number of cones so formed.
A cone and a hemisphere have the same base and the same height. Find the ratio between their volumes.
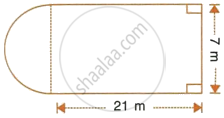
The horizontal cross-section of a water tank is in the shape of a rectangle with semi-circle at one end, as shown in the following figure. The water is 2.4 metres deep in the tank. Calculate the volume of water in the tank in gallons.
A solid is in the form of a right circular cone mounted on a hemisphere. The diameter of the base of the cone, which exactly coincides with hemisphere, is 7 cm and its height is 8 cm. The solid is placed in a cylindrical vessel of internal radius 7 cm and height 10 cm. How much water, in cm3, will be required to fill the vessel completely?
Volume of a cone is 1232 cm3 and its height is 24 cm. Find the surface area of the cone. `( π = 22/7)`
The volume of a conical tent is 1232 m3 and the area of the base floor is 154 m2. Calculate the: length of the canvas required to cover this conical tent if its width is 2 m.
The circumference of the base of a 10 m high conical tent is 44 metres. Calculate the length of canvas used in making the tent if the width of the canvas is 2m. (Take π = 22/7)
A vessel in the form of an inverted cone is filled with water to the brim: Its height is 20 cm and the diameter is 16.8 cm. Two equal solid cones are dropped in it so that they are fully submerged. As a result, one-third of the water in the original cone overflows. What is the volume of each of the solid cones submerged?
Water flows at the rate of 10 m per minute through a cylindrical pipe 5 mm of diameter. How much time would it take to fill a conical vessel whose diameter at he surface is 40 cm and depth is 24 cm?
