Advertisements
Advertisements
प्रश्न
The length, breadth, and height of a cuboid are in the ratio 5 : 3: 2. If its volume is 240 cm3; find its dimensions. Also, find the total surface area of the cuboid.
उत्तर
Let length of the given cuboid = 5x
Breadth of the given cuboid = 3x
Height of the given cuboid = 2x
Volume of the given cuboid = Length x Breadth x Height
= 5x x 3x x 2x = 30x3
But we are given volume = 240 cm3
30x3 = 240 cm3
⇒ x3 = `240/30`
⇒ x3 = 8
⇒ x = `8^(1/3)`
⇒ x = `(2 xx 2 xx 2)^(1/3)`
⇒ x = 2 cm
Length of the given cube = 5x = 5 x 2 = 10 cm
Breadth of the given cube = 3x = 3 x 2 = 6 cm
Height of the given cube = 2x = 2 x 2 = 4cm
Total surface area of the given cuboid = 2(l x b + b x h + h x l)
= 2(10 x 6 + 6 x 4 + 4 x 10) = 2(60 + 24 + 40) = 2 x 124
= 248 cm2
APPEARS IN
संबंधित प्रश्न
A plastic box 1.5 m long, 1.25 m wide and 65 cm deep, is to be made. It is to be open at the top. Ignoring the thickness of the plastic sheet, determine:
(i) The area of the sheet required for making the box.
(ii) The cost of sheet for it, if a sheet measuring 1 m2 costs Rs 20.
The paint in a certain container is sufficient to paint an area equal to 9.375 m2. How many bricks of dimensions 22.5 cm × 10 cm × 7.5 cm can be painted out of this container?
Daniel is painting the walls and ceiling of a cuboidal hall with length, breadth, and height of 15 m, 10 m, and 7 m, respectively. From each can of paint, 100 m2 of area is painted. How many cans of paint will she need to paint the room?
Find the lateral surface area and total surface area of a cube of edge 10 cm.
The length and breadth of a hall are in the ratio 4: 3 and its height is 5.5 metres. The cost of decorating its walls (including doors and windows) at Rs. 6.60 per square metre is Rs. 5082. Find the length and breadth of the room.
A milk container is 8 cm long and 50 cm wide. What should be its height so that it can hold 4 litres of milk?
How many wooden cubical blocks of side 25 cm can be cut from a log of wood of size 3 m by 75 cm by 50 cm, assuming that there is no wastage?
The weight of a metal block of size 5 cm by 4 cm by 3 cm is 1 kg. Find the weight of a block of the same metal of size 15 cm by 8 cm by 3 cm.
A water tank is 3 m long, 2 m broad and 1 m deep. How many litres of water can it hold?
How many bricks each of size 25 cm × 10 cm × 8 cm will be required to build a wall 5 m long, 3 m high and 16 cm thick, assuming that the volume of sand and cement used in the construction is negligible?
A rectangular field is 70 m long and 60 m broad. A well of dimensions 14 m × 8 m × 6 m is dug outside the field and the earth dug-out from this well is spread evenly on the field. How much will the earth level rise?
The rainfall on a certain day was 6 cm. How many litres of water fell on 3 hectares of field on that day?
The breadth of a room is twice its height, one half of its length and the volume of the room is 512 cu. dm. Find its dimensions.
A closed iron tank 12 m long, 9 m wide and 4 m deep is to be made. Determine the cost of iron sheet used at the rate of Rs 5 per metre sheet, sheet being 2 m wide.
A field is 150 m long and 100 m wide. A plot (outside the field) 50 m long and 30 m wide is dug to a depth of 8 m and the earth taken out from the plot is spread evenly in the field. By how much is the level of field raised?
The length of the longest rod that can be fitted in a cubical vessel of edge 10 cm long, is
The sum of the length, breadth and depth of a cuboid is 19 cm and its diagonal is ` 5 sqrt(5)` cm. Its surface area is
If V is the volume of a cuboid of dimensions x, y, z and A is its surface area, then `A/V`
Length, breadth and height of a cuboid shape box of medicine is 20 cm, 12 cm and 10 cm respectively. Find the surface area of vertical faces and total surface area of this box.
A closed rectangular box is made of wood of 1.5 cm thickness. The exterior length and breadth are respectively 78 cm and 19 cm, and the capacity of the box is 15 cubic decimeters. Calculate the exterior height of the box.
The breadth and height of a rectangular solid are 1.20 m and 80 cm respectively. If the volume of the cuboid is 1.92 m3; find its length.
The dining-hall of a hotel is 75 m long; 60 m broad and 16 m high. It has five – doors 4 m by 3 m each and four windows 3 m by 1.6 m each. Find the cost of :
(i) papering its walls at the rate of Rs.12 per m2;
(ii) carpetting its floor at the rate of Rs.25 per m2.
Find the area of metal-sheet required to make an open tank of length = 10 m, breadth = 7.5 m and depth = 3.8 m.
The floor of a rectangular hall has a perimeter 250 m. If the cost of painting the four walls at the rate of ₹ 10 per m2 is ₹ 15,000, find the height of the hall.
A matchbox is 4 cm long, 2.5 cm broad, and 1.5 cm in height. Its outer sides are to be covered exactly with craft paper. How much paper will be required to do so?
The length and breadth of a cuboid are 20 cm and 15 cm respectively. If its volume is 2400 cm3, find its height.
375 persons can be accommodated in a room whose dimensions are in the ratio of 6 : 4 : 1. Calculate the area of the four walls of the room if the each person consumes 64m3 of air.
The dimensions of a cuboidal box are 6 m × 400 cm × 1.5 m. Find the cost of painting its entire outer surface at the rate of ₹ 22 per m2.
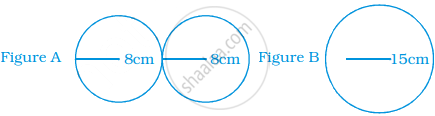
Below are the drawings of cross sections of two different pipes used to fill swimming pools. Figure A is a combination of 2 pipes each having a radius of 8 cm. Figure B is a pipe having a radius of 15 cm. If the force of the flow of water coming out of the pipes is the same in both the cases, which will fill the swimming pool faster?