Advertisements
Advertisements
प्रश्न
There are four men and six women on the city council. If one council member is selected for a committee at random, how likely is it that it is a woman?
उत्तर
There are four men and six women in the city council.
Ways of selected one of them = `""^10"C"_1`
∴ Total number of possible outcomes = 10
There are total 6 women. Ways of choosing one of them = 6
Number of favourable outcomes = 6
Probability of a woman being selected = `6/10 = 3/5`
APPEARS IN
संबंधित प्रश्न
Which of the following can not be valid assignment of probabilities for outcomes of sample space S = {ω1, ω2,ω3,ω4,ω5,ω6,ω7}
| Assignment | ω1 | ω2 | ω3 | ω4 | ω5 | ω6 | ω7 |
| (a) | 0.1 | 0.01 | 0.05 | 0.03 | 0.01 | 0.2 | 0.6 |
| (b) | `1/7` | `1/7` | `1/7` | `1/7` | `1/7` | `1/7` | `1/7` |
| (c) | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 |
| (d) | –0.1 | 0.2 | 0.3 | 0.4 | -0.2 | 0.1 | 0.3 |
| (e) | `1/14` | `2/14` | `3/14` | `4/14` | `5/14` | `6/14` | `15/14` |
A card is selected from a pack of 52 cards.
- How many points are there in the sample space?
- Calculate the probability that the card is an ace of spades.
- Calculate the probability that the card is
- an ace
- black card.
In a lottery, person chooses six different natural numbers at random from 1 to 20, and if these six numbers match with the six numbers already fixed by the lottery committee, he wins the prize. What is the probability of winning the prize in the game? [Hint: order of the numbers is not important.]
Fill in the blank in following table:
| P(A) | P(B) | P(A ∩ B) | P(A ∪ B) |
| `1/3` | `1/5` | `1/15` | .... |
A box contains 10 red marbles, 20 blue marbles and 30 green marbles. 5 marbles are drawn from the box, what is the probability that all will be blue?
Two unbiased dice are thrown. Find the probability that the total of the numbers on the dice is greater than 10.
Two unbiased dice are thrown. Find the probability that neither a doublet nor a total of 8 will appear
In a lottery, a person chooses six different numbers at random from 1 to 20, and if these six numbers match with six number already fixed by the lottery committee, he wins the prize. What is the probability of winning the prize in the game?
Which of the cannot be valid assignment of probability for elementary events or outcomes of sample space S = {w1, w2, w3, w4, w5, w6, w7}:
| Elementary events: | w1 | w2 | w3 | w4 | w5 | w6 | w7 |
| (ii) |
\[\frac{1}{7}\]
|
\[\frac{1}{7}\]
|
\[\frac{1}{7}\]
|
\[\frac{1}{7}\]
|
\[\frac{1}{7}\]
|
\[\frac{1}{7}\]
|
\[\frac{1}{7}\]
|
Which of the cannot be valid assignment of probability for elementary events or outcomes of sample space S = {w1, w2, w3, w4, w5, w6, w7}:
| Elementary events: | w1 | w2 | w3 | w4 | w5 | w6 | w7 |
| (iv) |
\[\frac{1}{14}\]
|
\[\frac{2}{14}\]
|
\[\frac{3}{14}\]
|
\[\frac{4}{14}\]
|
\[\frac{5}{14}\]
|
\[\frac{6}{14}\]
|
\[\frac{15}{14}\]
|
In a single throw of three dice, find the probability of getting the same number on all the three dice.
A box contains 100 bulbs, 20 of which are defective. 10 bulbs are selected for inspection. Find the probability that: all 10 are defective
A box contains 100 bulbs, 20 of which are defective. 10 bulbs are selected for inspection. Find the probability that all 10 are good
Two dice are thrown together. The probability that neither they show equal digits nor the sum of their digits is 9 will be
An urn contains twenty white slips of paper numbered from 1 through 20, ten red slips of paper numbered from 1 through 10, forty yellow slips of paper numbered from 1 through 40, and ten blue slips of paper numbered from 1 through 10. If these 80 slips of paper are thoroughly shuffled so that each slip has the same probability of being drawn. Find the probabilities of drawing a slip of paper that is numbered 5, 15, 25, or 35
The accompanying Venn diagram shows three events, A, B, and C, and also the probabilities of the various intersections (for instance, P(A ∩ B) = .07). Determine `P(B ∩ barC)`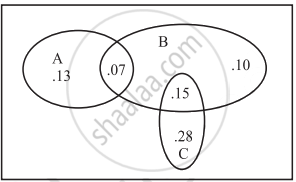
The accompanying Venn diagram shows three events, A, B, and C, and also the probabilities of the various intersections (for instance, P(A ∩ B) = .07). Determine `P(A ∩ barB)`
The accompanying Venn diagram shows three events, A, B, and C, and also the probabilities of the various intersections (for instance, P(A ∩ B) = .07). Determine Probability of exactly one of the three occurs
A bag contains 8 red and 5 white balls. Three balls are drawn at random. Find the probability that all one ball is red and two balls are white
If the letters of the word ASSASSINATION are arranged at random. Find the probability that two I’s and two N’s come together
If the letters of the word ASSASSINATION are arranged at random. Find the probability that all A’s are not coming together
If the letters of the word ASSASSINATION are arranged at random. Find the probability that no two A’s are coming together
Seven persons are to be seated in a row. The probability that two particular persons sit next to each other is ______.
6 boys and 6 girls sit in a row at random. The probability that all the girls sit together is ______.
A single letter is selected at random from the word ‘PROBABILITY’. The probability that it is a vowel is ______.
The probability that a person visiting a zoo will see the giraffee is 0.72, the probability that he will see the bears is 0.84 and the probability that he will see both is 0.52.
The probability that a student will pass his examination is 0.73, the probability of the student getting a compartment is 0.13, and the probability that the student will either pass or get compartment is 0.96.
If A and B are two candidates seeking admission in an engineering College. The probability that A is selected is .5 and the probability that both A and B are selected is at most .3. Is it possible that the probability of B getting selected is 0.7?
The sum of probabilities of two students getting distinction in their final examinations is 1.2
If 4-digit numbers greater than 5,000 are randomly formed from the digits 0, 1, 3, 5, and 7, what is the probability of forming a number divisible by 5 when, the repetition of digits is not allowed?
