Advertisements
Advertisements
प्रश्न
Write the mathematical formula for Bohr magneton for an electron revolving in nth orbit.
उत्तर
Bohr Magneton = `(eh)/(4pim_e)`
APPEARS IN
संबंधित प्रश्न
Obtain an expression for the orbital magnetic moment of an electron rotating about the nucleus in an atom.
An electron in an atom is revolving around the nucleus in a circular orbit of a radius of 5.3 x 10-11 m, with a speed of 2 x 106 m/s. Find the resultant orbital magnetic moment and angular momentum of the electron. [e = 1.6 x 10-19 C, me= 9.1 x 10-31 kg]
The electron in the hydrogen atom is moving with a speed of 2.5 × 106 m/s in an orbit of a radius of 0.5 Å. What is the Magnetic moment of the revolving electron?
Explain the origin of magnetism in material, hence find a magnetic moment of an electron revolving around the nucleus of an atom.
If M0 and L0 denote the orbital angular moment and the angular momentum of the electron due to its orbital motion, then the gyromagnetic ratio is given by ______
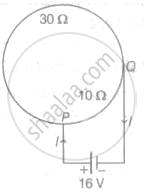
A circular coil of radius R has a resistance of 40 Ω. Figure shows two points P and Q on the circumference separated by a distance `(pi"R")/2`, which are connected to a 16 V battery with internal resistance of 0.5 Ω. What is the value of current I flowing through the circuit?
The magnetic moment of electrons due to orbital motion is proportional to ______.
(n = principal quantum numbers)
The S.I. unit of gyromagnetic ratio is ______
The Gyromagnetic ratio of the electron revolving in a circular orbit of a hydrogen atom is 8.8 x 1010 C kg-1. What is the mass of the electron? (Given charge of the electron = 1.6 x 10-19 C.)
The angle made by orbital angular momentum of electron with the direction of the orbital magnetic moment is ______.
An electron revolving in a circular orbit of radius 'r' with velocity 'v' and frequency v has orbital magnetic moment 'M'. If the frequency of revolution is tripled then the new magnetic moment will be ____________.
Which one of the following proportionality represents the relation between orbital magnetic moment M0 and orbital angular momentum L0 of an electron?
An electron revolving in a circular orbit of radius 'r' with velocity 'V' and frequency 'v' has orbital magnetic moment 'M'. If the frequency of revolution is doubled then the new magnetic moment will be ____________.
An electron of charge 'e' is revolving in a fixed orbit of radius 'r' with frequency 'f'. Its magnetic dipole moment is ____________.
The electron in hydrogen atom is moving in an orbit of radius 0.53 Å. It takes 1.571 x 10-16 s to complete one revolution. The velocity of electron will be `pi` = 3.142.
In an atom, electron of charge (-e) perform U.C.M. around a stationary positively charged nucleus, with period of revolution 'T'. If 'r' is the radius of the orbit of the electron and 'v' is the orbital velocity, then the circulating current (I) is proportional to ____________.
The period of oscillation of a magnet in a vibration magnetometer is 2 sec. The period of oscillation of a magnet whose magnetic moment is four times that of the first magnet is ______.
Which of the following expression represents the relation between orbital magnetic moment and orbital angular momentum of an electron?
A bar magnet of magnetic moment M1 is cut into two pieces along its axis. The pieces are kept perpendicular to each other with their unlike poles in contact. The magnetic moment of the arrangement is M2. The ratio of M1/M2 is ______.
An electron in an atom is revolving around the nucleus in a circular orbit of radius 0.53 A, with a speed of 2 x 106 m/s. Find the resultant orbital magnetic moment and angular momentum of electron.(e = 1.6 x 10-19 C, m = 9.1 x 10-31 kg)
The electron in the hydrogen atom is moving with a speed at 2.3 x 106 m/s in an orbit of radius 0.53Å. Calculate the magnetic moment of the revolving electron.
