Advertisements
Advertisements
Prove that:
sec2θ + cosec2θ = sec2θ x cosec2θ
Concept: Trigonometric Identities
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 90 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
Concept: Heights and Distances
If the angle θ = –45° , find the value of tan θ.
Concept: Trigonometric Ratios of Complementary Angles
Prove that: If the angles of a triangle are 45° – 45° – 90°, then each of the perpendicular sides is \[\frac{1}{\sqrt{2}}\]times the hypotenuse.”
Concept: Angles in Standard Position
Eliminate θ, if
x = 3 cosec θ + 4 cot θ
y = 4 cosec θ – 3 cot θ
Concept: Trigonometric Identities
Prove that `(sinθ - cosθ + 1)/(sinθ + cosθ - 1) = 1/(secθ - tanθ)`
Concept: Trigonometric Identities
Two buildings are in front of each other on a road of width 15 meters. From the top of the first building, having a height of 12 meter, the angle of elevation of the top of the second building is 30°.What is the height of the second building?
Concept: Heights and Distances
Four alternative answers for the following question are given. Choose the correct alternative and write its alphabet:
sin θ × cosec θ = ______
Concept: Trigonometric Identities
The volume of a cube is 1000 cm3. Find the side of a cube.
Concept: Surface Area and Volume of Three Dimensional Figures
A test tube has diameter 20 mm and height is 15 cm. The lower portion is a hemisphere. Find the capacity of the test tube. (π = 3.14)
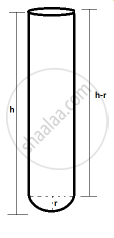
Concept: Surface Area and Volume of Different Combination of Solid Figures
Find the circumferences of a circle whose radius is 7 cm.
Concept: Circumference of a Circle
A toy is a combination of a cylinder, hemisphere and a cone, each with radius 10 cm as shown in the figure. Height of the conical part is 10 cm and total height is 60 cm. Find the total surface area of the toy.
(π=3.14, √2=1.41)
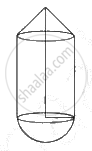
Concept: Surface Area and Volume of Different Combination of Solid Figures
Find the volume of a cone if the radius of its base is 1.5 cm and its perpendicular height is 5 cm.
Concept: Concept of Surface Area, Volume, and Capacity
Find the total surface area of a cylinder if the radius of its base is 5 cm and height is 40 cm.
Concept: Concept of Surface Area, Volume, and Capacity
The dimensions of a cuboid are 44 cm, 21 cm, 12 cm. It is melted and a cone of height 24 cm is made. Find the radius of its base.
Concept: Surface Area and Volume of Different Combination of Solid Figures
The radii of the ends of a frustum are 14 cm and 6 cm respectively and its height is 6 cm. Find its curved surface area.
Concept: Frustum of a Cone
The radius of a circle is 10 cm. The measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (\[\pi\]= 3.14 )
Concept: Length of an Arc
In the given figure, if A(P-ABC) = 154 cm2 radius of the circle is 14 cm, find
(1) `∠APC`
(2) l ( arc ABC) .
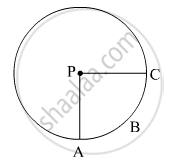
Concept: Circumference of a Circle
In the given figure, A is the center of the circle. ∠ABC = 45° and AC = 7√2 cm. Find the area of segment BXC.
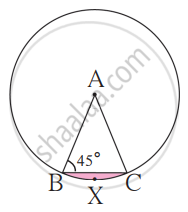
Concept: Areas of Sector and Segment of a Circle
Some plastic balls of radius 1 cm were melted and cast into a tube. The thickness, length and outer radius of the tube were 2 cm, 90 cm, and 30 cm respectively. How many balls were melted to make the tube?
Concept: Concept of Surface Area, Volume, and Capacity
