Advertisements
Advertisements
If ΔABC ~ ΔPQR, AB : PQ = 4 : 5 and A(ΔPQR) = 125 cm2, then find A(ΔABC).
Concept: Areas of Similar Triangles
In ΔABC, seg XY || side AC. If 2AX = 3BX and XY = 9, then find the value of AC.

Concept: Criteria for Similarity of Triangles
ΔABC ~ ΔPQR. In ΔABC, AB = 5.4 cm, BC = 4.2 cm, AC = 6.0 cm, AB:PQ = 3:2, then construct ΔABC and ΔPQR.
Concept: Areas of Similar Triangles
□ABCD is a parallelogram. Point P is the midpoint of side CD. seg BP intersects diagonal AC at point X, then prove that: 3AX = 2AC
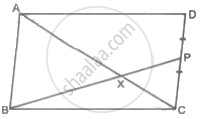
Concept: Criteria for Similarity of Triangles
Prove that, The areas of two triangles with the same height are in proportion to their corresponding bases. To prove this theorem start as follows:
- Draw two triangles, give the names of all points, and show heights.
- Write 'Given' and 'To prove' from the figure drawn.
Concept: Properties of Ratios of Areas of Two Triangles
From the information given in the figure, determine whether MP is the bisector of ∠KMN.
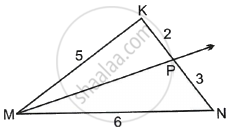
Concept: Property of an Angle Bisector of a Triangle
In the figure with ΔABC, P, Q, R are the mid-points of AB, AC and BC respectively. Then prove that the four triangles formed are congruent to each other.
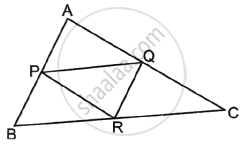
Concept: Criteria for Similarity of Triangles
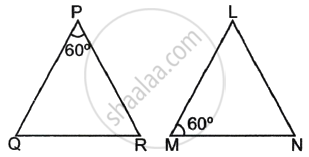
If ΔABC ∼ ΔDEF such that ∠A = 92° and ∠B = 40°, then ∠F = ?
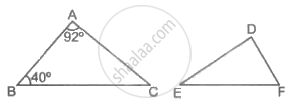
Concept: Property of an Angle Bisector of a Triangle
In the adjoining figure, ΔADB ∼ ΔBDC. Prove that BD2 = AD × DC.
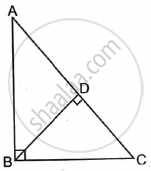
Concept: Areas of Similar Triangles
In the given figure, ΔPQR is a right-angled triangle with ∠PQR = 90°. QS is perpendicular to PR. Prove that pq = rx.

Concept: Criteria for Similarity of Triangles
Use area theorem of similar triangles to prove congruency of two similar triangles with equal areas.
Concept: Areas of Similar Triangles
Find the length of ST, if ΔPQR ∼ ΔPST.

Concept: Areas of Similar Triangles
In the given figure, ΔLMN is similar to ΔPQR. To find the measure of ∠N, complete the following activity.
Given: ΔLMN ∼ ΔPQR
Since ΔLMN ∼ ΔPQR, therefore, corresponding angles are equal.
So, ∠L ≅ `square`
⇒ ∠L = `square`
We know, the sum of angles of a triangle = `square`
∴ ∠L + ∠M + ∠N = `square`
Substituting the values of ∠L and ∠M in equation (i),
`square` + `square` + ∠N = `square`
∠N + `square` = `square`
∠N = `square` – `square`
∠N = `square`
Hence, the measure of ∠N is `square`.
Concept: Criteria for Similarity of Triangles
If ΔABC ∼ ΔDEF, length of side AB is 9 cm and length of side DE is 12 cm, then find the ratio of their corresponding areas.
Concept: Properties of Ratios of Areas of Two Triangles
Construct an equilateral triangle of side 7 cm. Now, construct another triangle similar to the first triangle such that each of its sides are `5/7` times of the corresponding sides of the first triangle.
Concept: Basic Proportionality Theorem (Thales Theorem)
In the given figure, S is a point on side QR of ΔPQR such that ∠QPR = ∠PSR. Use this information to prove that PR2 = QR × SR.
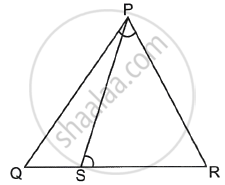
Concept: Criteria for Similarity of Triangles
A tangent ADB is drawn to a circle at D whose centre is C. Also, PQ is a chord parallel to AB and ∠QDB = 50°. Find the value of ∠PDQ.

Concept: Criteria for Similarity of Triangles
If the perimeter of two similar triangles is in the ratio 2 : 3, what is the ratio of their sides?
Concept: Areas of Similar Triangles
The sum of two angles of a triangle is 150°, and their difference is 30°. Find the angles.
Concept: Criteria for Similarity of Triangles
In the figure, PQ ⊥ BC, AD ⊥ BC. To find the ratio of A(ΔPQB) and A(ΔPBC), complete the following activity.
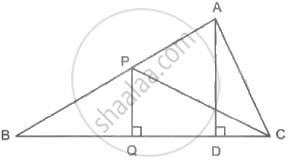
Given: PQ ⊥ BC, AD ⊥ BC
Now, A(ΔPQB) = `1/2 xx square xx square`
A(ΔPBC) = `1/2 xx square xx square`
Therefore,
`(A(ΔPQB))/(A(ΔPBC)) = (1/2 xx square xx square)/(1/2 xx square xx square)`
= `square/square`
Concept: Properties of Ratios of Areas of Two Triangles
