Relationship Between Radius and Diameter

1. Understand the Definitions:
The diameter (d) of a circle is defined as the longest distance across the circle, passing through the center. It connects two points on the circle.
The radius (r) of a circle is defined as the distance from the centre of the circle to any point on its circumference.

2. Visualise the circle:
Imagine a circle with a centre point. Draw a line from the centre to the edge of the circle. This line represents the radius (r).
Now, draw a line that passes through the centre and touches both ends of the circle. This line represents the diameter (d).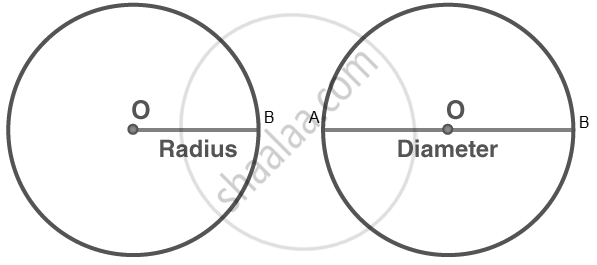           

3. Relate Radius to Diameter:
If you consider the diameter, it is made up of two radii. That is, if you start from one edge of the circle, go to the centre (which is one radius), and then from the centre to the other edge (which is another radius).
Therefore, the diameter can be expressed as the sum of two radii:   d = r + r

4. Simplify the equation:
Since r + r  is the same as 2r, we can rewrite the equation as d = 2r.

5. Conclusion:
The relation between the radius and diameter of a circle is: d = 2r
The diameter of a circle is twice the length of its radius.