Advertisements
Advertisements
प्रश्न
A, B and C have co-ordinates (0, 3), (4, 4) and (8, 0) respectively. Find the equation of the line through A and perpendicular to BC.
उत्तर
Slope of BC = `(0 - 4)/(8 - 4) = (-4)/4 = -1`
Slope of line perpendicular to BC = `(-1)/"slope of BC" = 1`
The equation of the line through A and perpendicular to BC is given by:
y − y1 = m(x − x1)
y − 3 = 1(x − 0)
y − 3 = x
y = x + 3
APPEARS IN
संबंधित प्रश्न
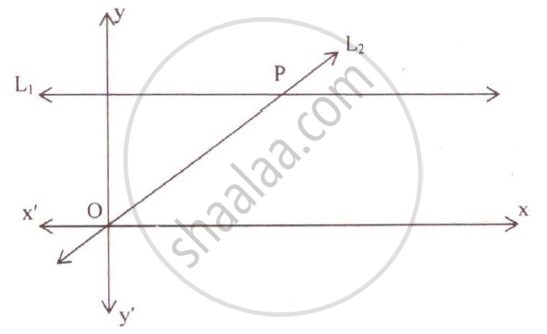
Given the equation of line L, is y = 4.
(1) Write the slope of line L2, if L2, is the bisector of angle O.
(2) Write the co–ordinates of point P.
(3) Find the equation of L2.
Does the line 3x − 5y = 6 bisect the join of (5, −2) and (−1, 2)?
Find the equation of a line whose : y-intercept = −1 and inclination = 45°
A line intersects x-axis at point (−2, 0) and cuts off an intercept of 3 units from the positive side of y-axis. Find the equation of the line.
Find the value of p if the line 3y = 5x - 7 passes through the point (p,6).
P is a point on the line segment AB dividing it in the ratio 2 : 3. If the coordinates of A and Bare (-2,3) and (8,8), find if Plies on the line 7x - 2y =4.
Find the inclination of a line whose gradient is 0.4663
Find the equation of a line whose slope and y-intercept are m = 2, c = -5
Find the equation of a line passing through the intersection of x + 2y + 1= 0 and 2x - 3y = 12 and perpendicular to the line 2x + 3y = 9
Find the equation of a line which is inclined to x axis at an angle of 60° and its y – intercept = 2.
